Si usted estudia el Coeficiente de Determinación R2 su texto de estadística simplemente le va a decir que es:
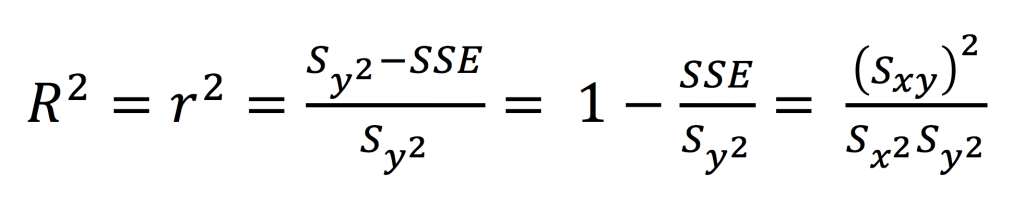No se preocupe si de momento no entiende nada y no le encuentra sentido. Como toda fórmula, hay una historia y un desarrollo detrás que se debe explicar para darle un valor práctico, y en el caso del Coeficiente de Determinación definitivamente es uno de los valores de mayor uso en toda la estadística.
R2 es una medida de qué tan bueno es su modelo para explicar lo que se está estudiando o analizando. Claro en estadística siempre hay que decir las cosas de la forma más elegante. En este caso diremos que el coeficiente de correlación es:
“La proporción de variación en la respuesta (variable y) que está explicado por el modelo, o sea por las variables independientes.”
Se usa tanto en regresión como en ANOVA, lo cual quiere decir que es importantísimo cuando se complementa el análisis de efectos con el análisis estadístico en las diferentes técnicas de Diseño de Experimentos (DoE).
Por último antes de hacer el primer ejemplo, vamos a usar solamente la siguiente fórmula (en español) para el Coeficiente de Determinación:
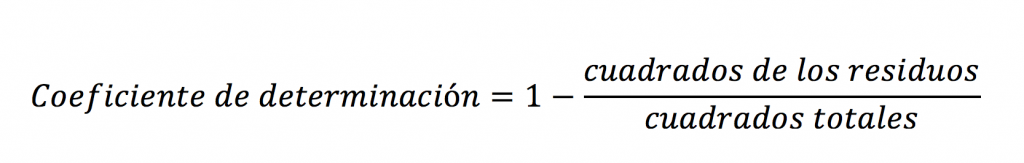Vamos a modificar un experimento del gran Douglas Montgomery (los que usamos la estadística como herramienta en nuestra vida diaria tenemos nuestros propios Messi, Michael Jordan, etc. …):
Se estudian tres marcas de baterías. Se sospecha que las vidas (en semanas) de las tres marcas son diferentes. ¿En qué porcentaje (proporción) explican las marcas la vida en semanas de las baterías?
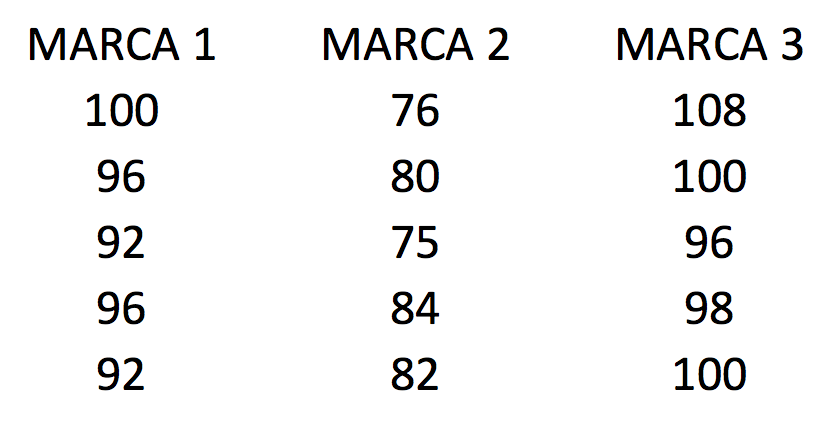
Siempre es bueno graficar para darse una primera impresión de lo que andamos buscando. En este caso un buen box plot nos dará las primeras pistas.
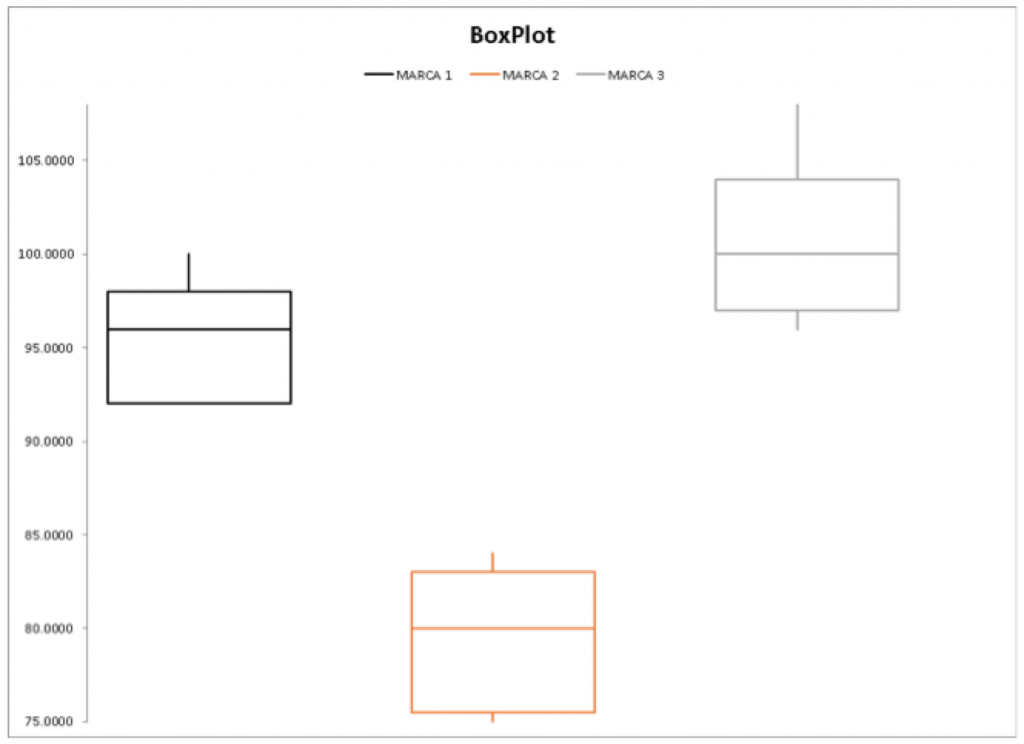Al separar la vida de las baterías por marca notamos diferencias fácilmente visibles entre las tres. Veamos si el coeficiente de determinación nos ayuda a explicar las diferencias.
Primero vamos a calcular la suma total de cuadrados. Para hacer este cálculo primero necesitamos calcular el promedio de todos los datos. Este número es 91.67. Además necesitamos los residuos y residuos cuadrados. Los residuos se calculan restando a cada dato el promedio, y ese número al cuadrado es el residuo cuadrado.
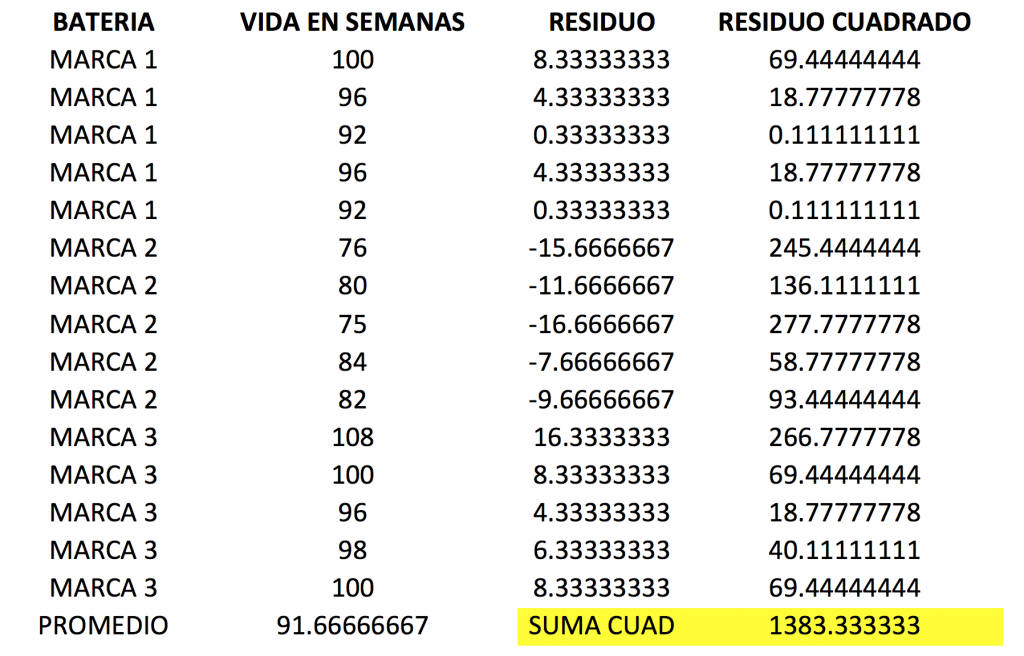Y finalmente la suma total de cuadrados es 1,383.33. Este último número lo podemos considerar una estimación de la variación de los datos, sin embargo no tiene mucho sentido práctico.
Ahora, ¿qué pasa si separamos la suma de cuadrados de cada una de las marcas?
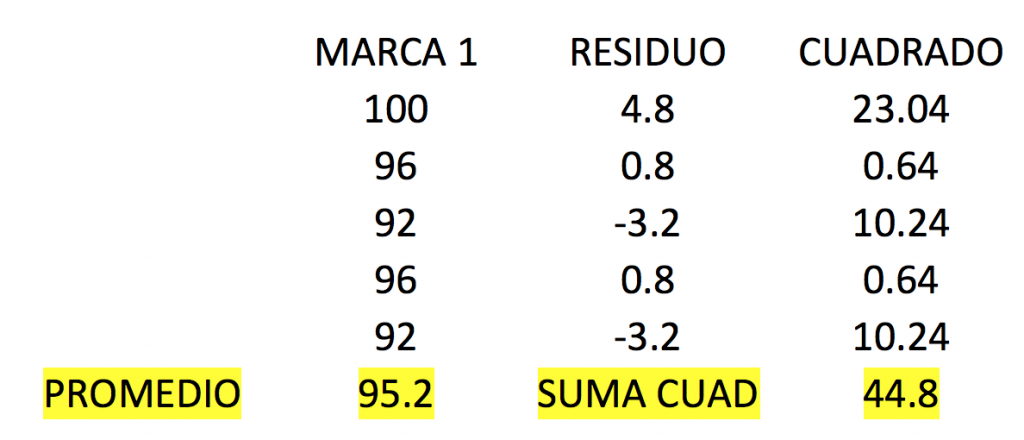
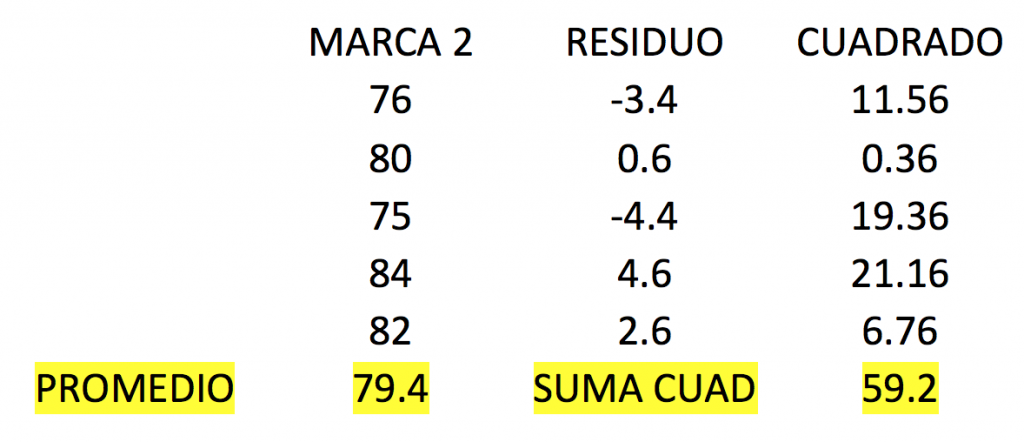
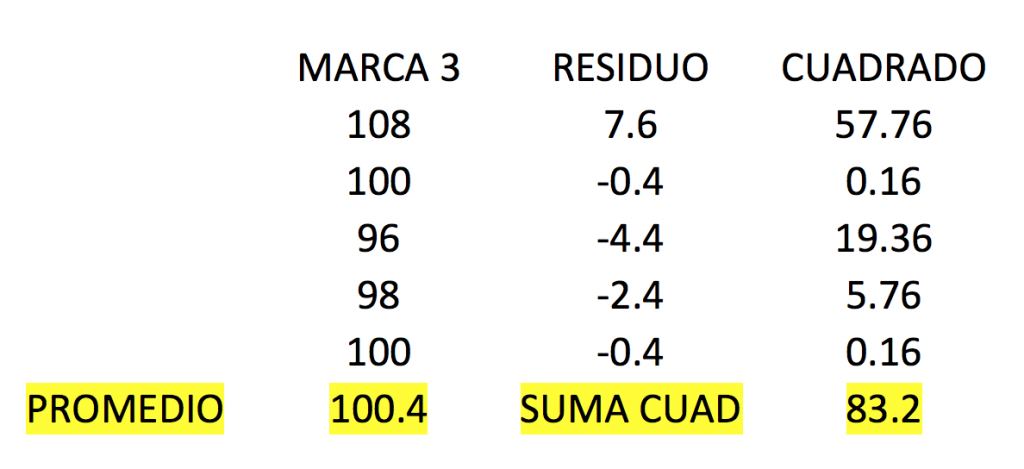La suma de cuadrados de cada marca la podemos considerar un estimado de la variación de cada una.
Si sumamos el resultado de los cuadrados de cada marca tenemos:
44.8 + 59.2 + 83.2 = 187.2
44.8, 59.2 y 83.2 explican la variación POR SEPARADO de las tres marcas. ¿Qué tanto explican la variación las marcas? Aquí es donde entra el coeficiente de determinación. Recuerda la fórmula:
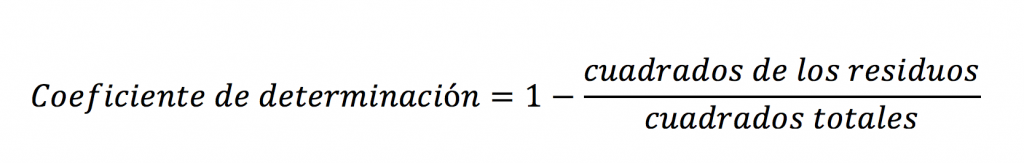
Precisamente tenemos todos los elementos para usarla:
Cuadrados de los residuos (la suma de los cuadrados por separado) = 187.2
Cuadrados totales (el primer cálculo que incluía a todos los residuos) = 1,383.33
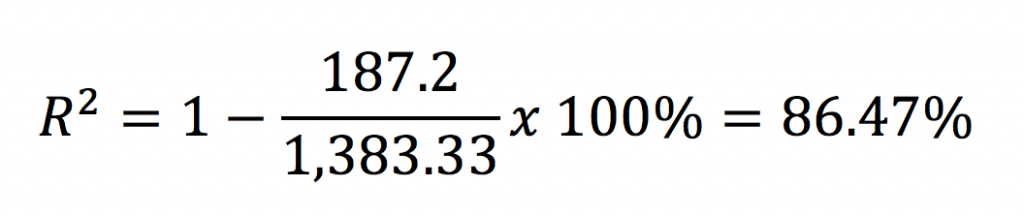Separar la variación por marca explica un 86.47% de la variación en el tiempo de duración. Dicho más sencillo modelar la vida de las baterías usando las marcas explica el tiempo de vida en un 86.47%
COEFICIENTE DE DETERMINACIÓN AJUSTADO
El coeficiente de determinación ajustado es una corrección que toma en cuenta el tamaño de muestra y el número de parámetros en el modelo. Siempre es menor que R2 de esta manera no puede “forzarse” a llegar a ser 1 con sólo agregar más variables.
Los grados de libertad totales se calculan restando 1 al total de datos (en este caso 15 datos menos 1 = 14 grados de libertad).
Los grados de libertad del error se calculan restando 1 a cada grupo de datos ( en este caso cada set de datos tiene 5 datos – 1 = 4 por set, por 3 grupos de datos = 4 x 3 = 12 grados de libertad.
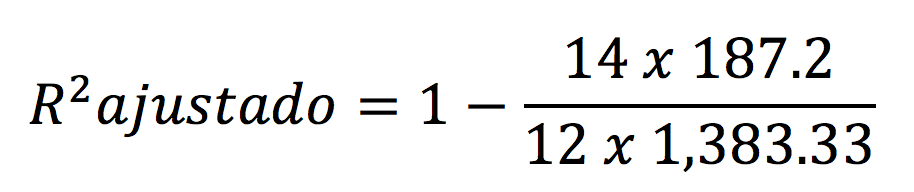El resultado es 84.21%.
El R2 ajustado siempre es menor que el R2.
¿SON LOS R2 BAJOS NECESARIAMENTE INDICATIVOS DE UN MAL MODELO?
No siempre un coeficiente de determinación bajo es malo. Por ejemplo suponga que está prediciendo el comportamiento de compra de sus clientes y su modelo le dice que R2 es 54%. Comportamientos humanos son muy difíciles de modelar y más bien un número entre 50% y 60% suele ser considerado muy bueno.
Lo mismo se puede decir de los valores altos, no necesariamente siempre son buenos, pero esa es historia para otro blog (y requiere de otros conocimientos estadísticos más complejos). Y dado que hemos mencionado ANOVA (Análisis de Varianza) un par de veces, el próximo blog estadístico tratará sobre esta prueba importantísima en el Análisis Estadístico.
