Hay una conocida canción de los años 80 de una banda Sudamericana llamada Enanitos Verdes, que para muchos que rondamos los 40 y tantos pues nos es conocida y en ocasiones escucharla nos trae gratos recuerdos de adolescencia. El coro, que es una parte de la canción dice así:
Vagando por las calles, El extraño de pelo largo sin preocupaciones va…. Hay fuego en su mirada y un poco de insatisfacción, por esa mujer que siempre quiso y nunca pudo amar, jamás jamás…[1]
En este punto de lectura, usted se preguntará que implicación tiene esa canción versus el concepto que puse en el título del artículo, sobre todo la palabra “transformando”.
Como usted sabe la transformación de datos es un procedimiento matemático muy común en la estadística que busca que algo que no sigue una distribución Gaussiana o Normal pues pueda aplicársele tratamientos estadísticos basados en la Distribución Normal.
Los beneficios de trabajar con la Normal son muchos, una importante parte de los concetos matemáticos modernos descansa en que los datos sean normales, si no es así “en teoría” no se deberían aplicar estos tipos de tratamientos, sin embargo la cuestión de la normalidad no es tema tan común como muchos piensan, en veces pues simplemente los datos no son normales y que los datos no sean normales no debería implicar que usted empiece a sudar copiosamente o que el fantasma de la frustración lo invada, para nada, hay muchísimos comportamientos probabilísticos en los negocios, la naturaleza que no sigue la distribución normal. Le quiero mostrar al menos unos 4 ejemplos de cuestiones que no siguen la distribución normal y que están bien:
1- Vida útil de un bisturí quirúrgico (Distribución Weibull)
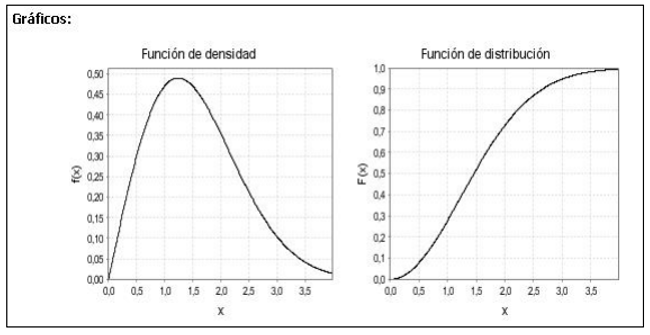
Fuente: https://www.sergas.es/Saude-publica/Documents/1899/Ayuda_Epidat_4_Distribuciones_de_probabilidad_Octubre2014.pdf
2- Crecimiento de la población mundial
[1] Si quiere ver el video actualizado de la canción entre acá: https://www.youtube.com/watch?v=6zu9GZ-_h4E
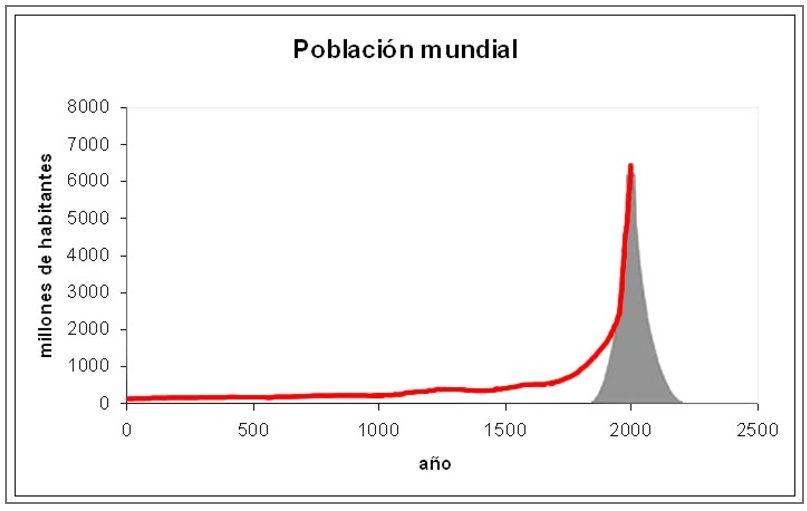
Fuente: http://www.decrecimiento.info/2013/11/decrecimiento-energetico.html
3- Tiempos de servicio (tiempo de descarga de barcos en el puerto) Distribución Erlang-k
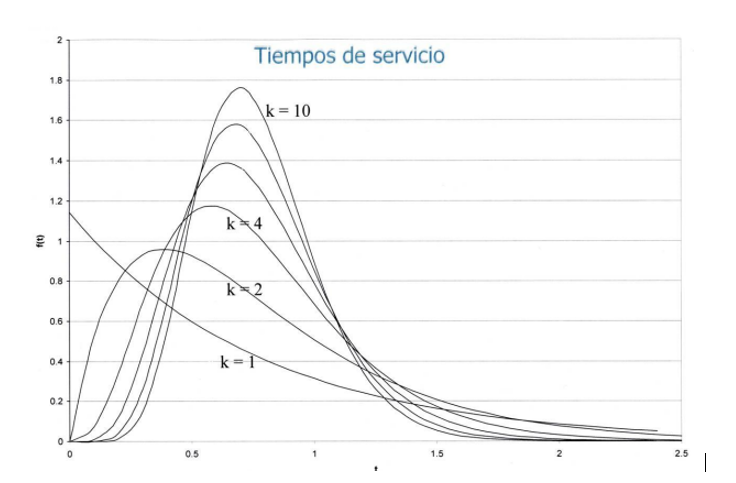
Fuente: http://www.graduadosportuaria.com.ar/Vias%20Navegables/Can_Tema%20%207_Teoria%20de%20colas_20130831.pdf
Como usted puede observar son procesos totalmente normales (no siguen la distribución normal pero sí siguen otra distribución). He llegado a la conclusión después de algunos años de experiencia de procesamiento de datos que primeramente el nombre “Distribución Normal” tienen a confundir a la gente. La palabra “normal” en estadística no significa lo que significa en por ejemplo el idioma español, así como ejemplo decir como adjetivo significa según la RAE:
- adj. Dicho de una cosa: Que se halla en su estado natural.
- adj. Habitual u ordinario.
- adj. Que sirve de norma o regla.
Como usted observará, pues esas tres definiciones distan mucho de lo que conocemos como una función matemática en forma de “campana”. De hecho, la Distribución Normal que también se le llama Distribución Gaussiana dado que uno de sus principales proponentes Carl Friedrich Gauss la empezó a utilizar fuertemente para cálculos astronómicos en 1794 sin embargo el primer proponente de esta fue Abraham de Moivre que desde 1733 la usó para analizar probabilidades. Por lo tanto, no hay que confundir y pensar que “Normal” significa que es una distribución que como indican los adjetivos de la RAE es “ordinaria” o es la “regla”; por el contrario, si analizamos la curva Gaussiana o Normal nos daremos cuenta de que es bastante rara en su composición, veamos por qué:
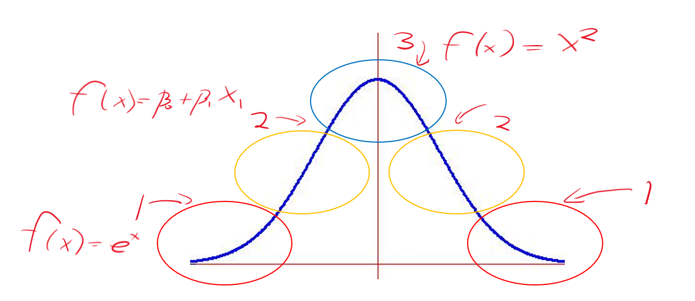
Fuente: los rayones de Franklin.
Como puede observar he señalado 3 áreas en la curva normal típica (la estandarizada con media de 0 y desviación de 1). Si observa a detalle las áreas 1 tiene un comportamiento creciente y decreciente acelerado, vienen desde menos infinito y siguen a más infinito, este comportamiento es muy típico de la función exponencial, seguidamente esta el área 2, que es muy lineal y finalmente la copa o parte alta que es el área 3 que se ve claramente que parece ser un tipo de cuadrática cóncava hacia abajo. El hecho de que existan esas 3 cuestiones juntas pues permite concluir algo bastante obvio, realmente la “Normal” no es tan “normal”, es algo así como un ornitorrinco estadístico si me permiten hacer la analogía.

Ciertamente en la práctica hay mucho comportamiento estadístico que siguen a la Gaussiana (prefiero decirle así que Normal), y que no solo en la naturaleza se presenta sino también en el mundo de los negocios sin embargo tampoco debemos obsesionarnos con que nuestros datos deban ser normales para procesarlos, de hecho, hay muchas estrategias que se pueden usar para tratar datos no normales.
El tema aquí, y que da fundamento a este artículo es la transformación de datos. La transformación de datos la hacemos entonces para permitir que datos no normales sean gaussianos. El aplicar alguna función matemática utilizando los datos originales como variable independiente “X” y generar una nueva “Y” que va a ser la variable transformada es algo común en muchos paquetes de software estadístico y que muchos green belts y black belts pueden usar a diario. El cuidado radica en, ¿cuándo realmente yo puedo transformar datos?
Primero empecemos por estar claros por qué un conjunto de datos no puede ser gaussiano o normal, básicamente hay dos razones:
1- La población de donde provienen los datos simplemente no sigue una normal, sigue una distribución probabilística diferente a la normal y eso esta bien, no todo en la vida “es normal”.
2- La otra razón, y la más preocupante, existen factores de ruido que afectan a los datos procesados o simplemente la variable que usted esta analizando esta fuera de control estadístico y por eso se ven “no normales”
No nos debe importar tanto la primera razón, al fin y al cambo si algo es diferente a lo habitual pues hay que respetarlo, la cuestión que si le debe preocupar es si usted cuenta con el conocimiento y la habilidad para saber interpretar que efectivamente se topó con algo que sigue otro comportamiento estadístico. En este punto no está mal “transformar datos”, sin embargo, encontrar una buena transformación es el tema, porque el error de transformación puede ser tal que ciertamente haga que tratar de transformar no sirva para nada. Veamos los siguientes datos de transformaciones de tiempos de reparación de máquinas que aprovechamos de nuestro Software Estadístico StatSolver (www.statsolver.net):
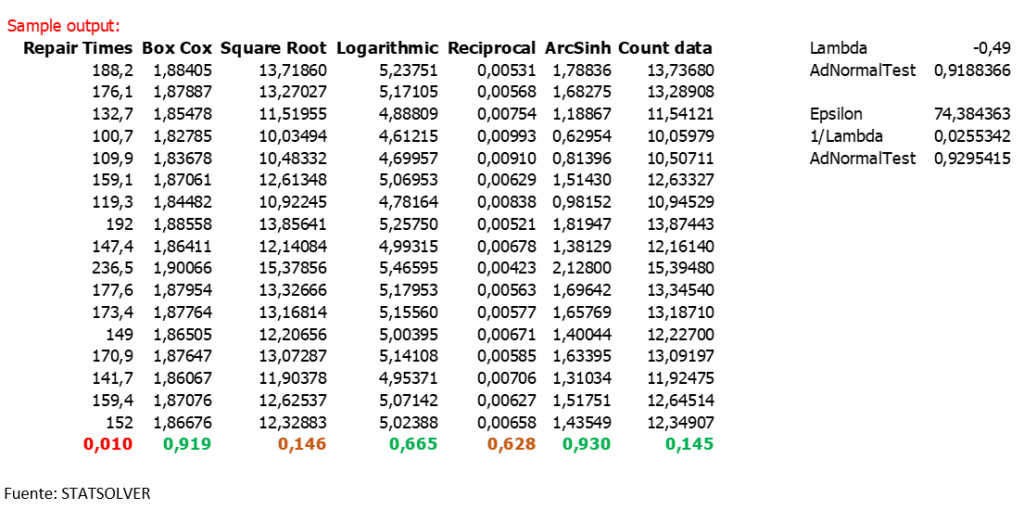
Primero veamos que el p-value al final de los datos es 0,010 lo que significa que los datos ciertamente no son normales, recuerde que la prueba de hipótesis es H0 datos normales contra H1 datos no normales, apliqué la prueba Anderson Darling y contrasté contra una significancia de 0,05 cualquier p-value debajo de 0,05 afirma que los datos son no normales. Uno diría, pues que las transformaciones dieron muy buen efecto, todos los demás p-values dieron normal con los modelos matemáticos Box Cox, Raíz cuadrada, Logarítmico, reciproco, Arcoseno hiperbólico
Por dicha, existen muchos paquetes estadísticos que nos puede permitir encontrar y aplicar modelos matemáticos adecuados para transformar la data, y que con respecto a la interpretación del p-value y de nuestra habilidad matemática puede permitirnos encontrar el conjunto de datos transformados para poder procesarlos mediante la Distribución Gaussiana.
La cuestión entonces que me preocupa es la segunda razón de por qué los datos no son normales, y es una que mucha gente pasa por alto. Es común que los datos se vean afectados por otros factores o que simplemente la variable en análisis este fuera de control. Estas afectaciones que generan otros factores o el mismo factor en análisis muchas veces pasan desapercibidas y por lo general implica el peor uso de una transformación posible. El transformar datos fuera de control o afectados por factores de ruido sin saber usted la razón es el equivalente a tener una enfermedad muy grave y tomarse una pastilla para el dolor (analgésico) y pensar por ello que está curado, posiblemente la razón del problema de salud siga y pueda agravarse, pero usted al no tener dolor no le preocupa. Una transformación puede convertirse en la “Panadol extrafuerte” de un grupo de datos que están mal, que están descontrolados o que los afectan muchas otras cosas, cosas que usted debería saber y debería sistémicamente tratar de solucionar antes de, pensar en transformar. Si usted transforma datos que están mal simplemente esta ignorando aspectos clave de su proceso que deben corregirse primeramente y estaría traicionando a la mejora continua el proceder de esa forma.
Por lo anterior, le recomiendo los siguientes pasos cuando piense en transformar:
- Este claro que no todo sigue el comportamiento gaussiano (curva normal) y que está bien que los datos en otros contextos sigan otra distribución probabilística.
- Cerciórese que el proceso esta bajo control estadístico, o sea que factores especiales o perturbadores estén controlados y solo exista variabilidad aleatoria.
- Si está claro que los datos están en control y siguen otra distribución de probabilidad explore el hecho de poder tratarlos según su modelo matemático correspondiente, existente muchísimos paquetes estadísticos que tiene analizadores de probabilidad que le dirán cuál es esa distribución.
- Recuerde que existente el campo de la Estadística No Paramétrica también, la que no depende de la normalidad, puede ser de gran ayuda para tratar la data con confiabilidad.
- Pruebe aumentar los tamaños de muestra y muestrear más frecuentemente, esto podría ayudar y en conjunto con el Teorema del Límite Central (sacar promedios de muestras y trabajar con estos) a que los datos pueden ser tratados a través de tratamientos estadísticos gaussianos.
Si ya nada de lo anterior le convence y quiere seguir con la transformación pues adelante, trate de valorar varios ajustes matemáticos para ver si encuentra un modelo que transforme adecuadamente la data y no se deje seducir por un p-value muy alto, pues nada hace con tener un muy buen ajuste normal con la transformación si el modelo matemático parece sacado de libro de Física Cuántica, no es un tema práctico ésto, es mejor p-values de transformación un poco más pequeños pero con modelos matemáticos más accesibles.
Finalmente, recuerde que una transformación de datos prácticamente es el último recurso que debemos aplicar y que tiene muchos cuidados e implicaciones su uso. Espero que esta información le sirva para sus futuros proyectos, y le dejo mi versión ñoña de la canción de los Enanitos Verdes del principio para que a usted no le pase el aplicar mal la transformación de datos:
Transformando por las calles, mirando a la gente trabajar…
El ingeniero de pelo largo sin preocupaciones va….
Hay fuego en su mirada y un poco de insatisfacción,
por esos datos que siempre quiso y nunca pudo transformar, jamás jamás…


