Iniciamos una nueva serie de publicaciones, esta vez sobre el tema del uso de las distribuciones de probabilidad.
Un compañero de trabajo de hace muchos en el ITCR, Mark Befeler, contaba que un profesor de la Universidad de Cornell invitaba a sus estudiantes a VER distribuciones de probabilidad en lugar de equipos, partes, llamadas, transacciones, procesos, filas, en fin, tanto como se pudiera. Aprenderemos en esta serie cómo podemos usar la teoría estadística en el día a día para hacer más fácil el cálculo, predicción y automatización del trabajo.

Foto: Random Showers por Matt (usuario de Flickr, ver perfil aquí).
La idea no es usar complicadísimas fórmulas matemáticas (que yo llamo fórmulas “dolor de panza”), ni listar las más de 170 distribuciones de probabilidad conocidas, inventadas, descubiertas, explicadas, hasta el momento. Más bien vamos a limitarnos a las distribuciones más comunes y usadas.
Un par de definiciones y un “problemón” cognitivo
Empecemos por definir probabilidad. Es la rama de la matemática que estudia que tan posible es que un evento aleatorio suceda.
Y una distribución de probabilidad es una función matemática que describe los posibles resultados que puede asumir una variable aleatoria con ciertas características.
Por ejemplo, en una muestra aleatoria de 100 personas podemos medir las estaturas y crear una distribución de estas. Este tipo de distribución es útil para luego determinar cuáles resultados se pueden esperar y qué tan probable es que sucedan.
Podemos ver como la probabilidad literalmente explica el funcionamiento natural, real y aleatorio del mundo, sin embargo, este concepto básico no es intuitivo para el cerebro que evolutivamente prefiere LA respuesta, EL resultado; prefiere explicaciones lineales y directas que una lista de potenciales resultados que pueden o no pasar.
Como primer ejemplo veamos la distribución el siguiente gráfico de la distribución de estaturas de los jugadores de la NBA en el año 2018.
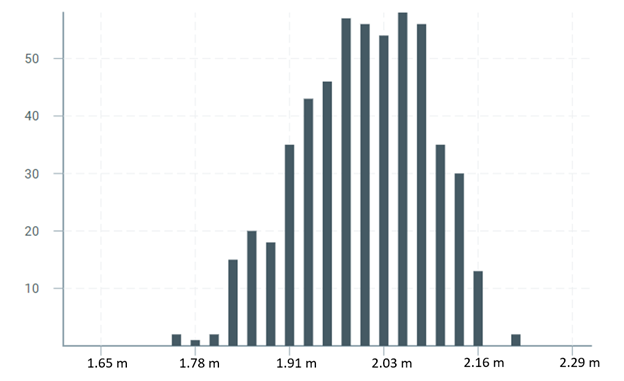
Estaturas de los jugadores de la NBA (National Basketball Association, USA) 2018
En los extremos podemos ver que solamente 5 de los 528 jugadores (0.6% de todos los jugadores medidos) miden menos de 1.80 metros, y que 15 jugadores miden más de 2.10 m. (2.4%). Alrededor del 50% de los jugadores miden entre 1.98 m. y 2.08 m. ¿De dónde salen estos números? Vea en las barras del gráfico la cantidad de jugadores correspondientes a cada estatura.
Basado en su estatura busque en el gráfico y prediga qué tan probable sería que lo llamaran de la NBA.
¿Para qué usamos las distribuciones de probabilidad en estadística?
La estadística se trata de explicar el mundo con un número reducido de cálculos y representaciones gráficas (entre menos mejor). El fabuloso Engineering Statistics Handbook del NIST (National Institute of Standards and Technology, de Estados Unidos) lista los siguientes usos prácticos de las distribuciones de probabilidad:
- Calcular intervalos de confianza para parámetros estadísticos [como promedio, desviación estándar y proporciones].
- Calcular regiones críticas para pruebas de hipótesis.
- Determinar un modelo de distribución razonable de los datos.
- Los intervalos estadísticos y las pruebas de hipótesis generalmente se basan en supuestos sobre distribuciones específicas.
- Estudios de simulación a partir de generación de números aleatorios muchas veces requieren del uso de distribuciones específicas.
Viendo de lo general a lo específico
Para llegar a los usos indicados en la lista anterior primero tenemos que definir qué clase de distribución puede modelar los fenómenos del día a día.
Lo más general es escoger entre dos grandes tipos:
- Distribuciones discretas para variables enteras y contables.
- Distribuciones continuas para variables que se miden con algún instrumento.
| Distribuciones discretas | Distribuciones continuas |
|
Todo lo que se puede contar: · Número de quejas de clientes. · Número de personas esperando por un servicio. · Número de hijos por pareja. · Cantidad de defectos en una unidad de producto. |
Todo lo que se mide con un instrumento de medición: · Estatura. · Peso. · Temperatura. · Velocidad. · Potencia. |
Tabla 1
Ejemplos de situaciones del día a día que siguen distribuciones discretas y continuas
Distribuciones discretas:
Solamente pueden tener valores discretos, o dicho más simplemente, números enteros.
No hay valores intermedios. No existe 1.5 hijos, ni 3.4 árboles. Por ejemplo, el número de televisores por casa en un país de América del Sur sigue la siguiente distribución de probabilidad:
| Número de televisores | Probabilidad |
| 0 | 0.05 |
| 1 | 0.15 |
| 2 | 0.25 |
| 3 o más | 0.55 |
Tabla 2
Distribución discreta de probabilidad (Número de televisores por casa)
Dos cosas importantes. “Cero televisores por casa” tiene una probabilidad asociada, 5% de las casas no tienen televisores; y 55% de las casas tienen 3 o más televisores. La mención del cero como parte de la distribución y el “3 o más” son términos importantes en el mundo de las distribuciones de probabilidad.
¿Cuál es la probabilidad de que una casa tenga uno o dos televisores?
Probabilidad de 1 o 2 televisores = Probabilidad de 1 televisor + Probabilidad de 2 televisores
= 0.15 + 0.25 = 0.40
Las distribuciones discretas más usadas
Las distribuciones discretas más usadas (y dónde las podemos ver) son las siguientes:
| Distribución | Definición | ¿Dónde la podemos ver? |
| Binomial | La probabilidad de ÉXITO o FALLO en un experimento que se repite múltiples veces. | · % de producto defectuoso en una línea de producción.
· % de clientes satisfechos (o insatisfechos) en una transacción.
· Pasar o perder un curso. |
| Poisson | Describe eventos en una población grande. Generalmente la población se puede entender como un rango (de tiempo, de área, de distancia, etc.) | · Número de defectos en una unidad de producto.
· Número de errores en un documento.
· Número de clientes que llaman a un centro de llamadas.
· Células que adquieran cierta mutación en una gran población de células. |
| Geométrica | Modelar el número de fallas antes de un éxito. | · Número de unidades que se deben inspeccionar hasta que aparezca una defectuosa.
· Número de días sin infecciones en un hospital hasta el primer día con al menos una infección.
· Número de años que su equipo de futbol no es campeón hasta que, finalmente, es campeón. |
| Hipergeométrica | Probabilidad de encontrar una característica de interés en una población finita y pequeña. | · Las primeras muestras que se envían cuando se está validando a un proveedor nuevo.
· Mi camisa favorita lista (lavada y planchada) exactamente el día que la necesito.
· Los trucos de un mago con juegos de cartas. |
| Uniforme discreta | Un número de resultados discretos finitos e igualmente probables de suceder. | · La lotería de Costa Rica.
· El lanzamiento de un dado.
· Seleccionar un estudiante al azar para que conteste una pregunta en una clase. |
Tabla 3
Principales distribuciones discretas de probabilidad
Distribuciones continuas:
Las distribuciones continuas se caracterizan porque pueden tomar cualquier valor (continuo). Hay infinito número de valores que la variable puede tomar. Es el caso del uso de instrumentos de medición para determinar cada valor.
El gráfico 1 es un ejemplo de distribución continua donde las estaturas pueden tomar cualquier valor como 1.93 metros, 1.925 metros, 1.99 metros, 1.9855 metros, etc.
Las distribuciones continuas más usadas
Las distribuciones continuas más usadas (y dónde las podemos ver) son las siguientes:
| Distribución | Definición | ¿Dónde la podemos ver? |
| Normal | Distribución continua es que simétrica a ambos lados del promedio. Llamada curva de la campana por el gráfico que genera. | · Estaturas de adultos.
· Errores de medidas.
· Medición de Cociente intelectual.
· Peso al nacer. |
| Exponencial | Distribución de probabilidad del tiempo entre eventos Poisson. | · El tiempo (iniciando en este momento) hasta que ocurra un terremoto.
· El tiempo de llamadas de larga distancia.
· Tiempo de duración de la batería de un vehículo.
· Muy útil para modelar tiempo entre fallas en confiabilidad. |
| Weibull | Familia de distribuciones que se usa principalmente para análisis de la vida de un producto, y que tiene la característica de que puede tomar cualquier forma lo que la hace muy versátil. | · Análisis de garantías de productos.
· Vida útil de productos.
· Tiempo que pasan los servicios públicos sin fallar.
· Cualquier situación en la que el tiempo entre fallas es importante. |
| Uniforme continua | Distribución continua donde los eventos tienen la misma probabilidad de ocurrir. | · El tiempo que tarda en llevar el elevador desde el momento que usted toca el botón.
· El peso de los autos de cierta categoría (por ejemplo, de dos puertas). |
Tabla 4
Principales distribuciones continuas de probabilidad
Desde las decisiones más básicas hasta las de mayor peso, siempre será posible beneficiarse del pensamiento probabilístico. Empiece a ver distribuciones de probabilidad en todo lo que hace, y verá que se le abre un nuevo mundo de mejores decisiones.


