En estadística nos encontramos con los grados de libertad en fórmulas y tablas. ¿Cuál es su origen e importancia? Veamos varias formas de explicar este importante concepto empezando por su forma más sencilla y natural de ver.

El número de datos independientes
Piense en los grados de libertad de la siguiente manera.
Un equipo de futbol tiene once jugadores, el entrenador ya ha dado la alineación del próximo partido, el día del juego, antes del inicio sale el primer jugador, puede ser cualquiera de los once; sale el segundo, puede ser cualquiera de los diez que quedan. Siguen saliendo y la afición se pregunta quién será el siguiente futbolista en asomarse por el camerino. Cuando los primeros diez jugadores han salido y solamente falta el último, ya no habrá sorpresa, todos saben quién es el que falta.
Los diez primeros jugadores son “libres” e independientes, pueden salir del camerino en cualquier orden, pero el número once no es libre, no es independiente. Este es un caso de n-1 grados de libertad.
Esta es la definición más general de grados de libertad, el número de observaciones en los datos que son libres de variar, y dicho más concretamente, que pueden variar cuando se estiman parámetros estadísticos, veamos.

Definición formal y cálculo básico
Grados de libertad es el número de piezas independientes de información en los datos que son libres de variar cuando se estiman parámetros.
En el promedio:
Suponga que tiene cinco datos para calcular un promedio por medio de la fórmula:
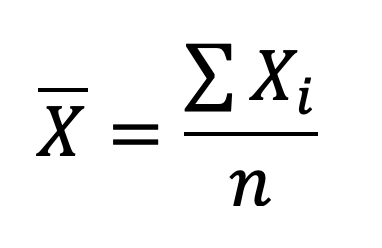
Si muestrea nuevamente con el mismo tamaño de muestra no se sorprenderá de obtener un nuevo estimado debido a la variabilidad aleatoria. Todos los datos en el cálculo del promedio son libres de variar.
Usted tiene el primer dato de su muestra de cinco, todavía le falta muestrear cuatro datos más y estos pueden tomar cualquier valor, por lo tanto, el valor de los grados de libertad del promedio de la muestra es n.
En la desviación estándar:
Cuando conocemos todos los valores de toda la población la desviación estándar es:
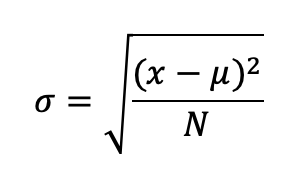
Necesitamos conocer todos los valores (N) para poder calcular la desviación estándar de la población.
En el caso de una muestra:

¿Por qué la desviación estándar de la muestra tiene diferentes grados de libertad?
En este caso no conocemos el promedio (de la población) sino que tenemos que estimarlo (de la muestra). Usemos las estaturas de los miembros de mi familia como ejemplo.
| 160 cm |
| 162 cm |
| 160 cm |
| 173 cm |
| 170 cm |
El promedio de la muestra es 165 cm
En este caso, cuatro datos son libres de variar, pero el quinto es fijo debido a la limitación impuesta por el promedio de 165 cm, el dato que falte tiene que llevarnos ese promedio. Esta restricción surge solamente si usamos el promedio muestral para calcular la desviación estándar. Si conociéramos la media de la población no habría ninguna restricción y todos los valores de la muestra serían libres de variar. Por esta razón el valor de los grados de libertad para la desviación estándar de la población es N, y n-1 para el valor de los grados de libertad de la desviación estándar de la muestra.
En la distribución t-student
La lógica es la misma del caso anterior.
Si estimamos el promedio con una muestra de tamaño n, y queremos hacer una prueba t de una muestra, tenemos la limitación del estimado del promedio de la muestra. Dado que el valor del promedio de la muestra ya ha sido calculado tendremos n-1 muestras libres (grados de libertad) y el último valor estará determinado por el promedio.
Y así podríamos seguir explicando caso por caso, distribución por distribución, técnica estadística por técnica estadística, y la base es siempre la misma, ¿cuántas observaciones son libres de variar según sea el caso?
William Gosset, el de la distribución de t-Student, y su mentor Sir Ronald Fisher, el papá del diseño de experimentos y la ANOVA, fueron quienes en sus casuales conversaciones definieron este importante concepto, con Fisher formalizando su autoría. ¡Gracias Maestros!
E!



