Estamos a pocas semanas del Campeonato Mundial de Futbol de Rusia 2018. La etapa previa significa una sola cosa, es tiempo del Álbum Panini. Para los ticos el álbum tiene un costo de 1,250 colones (US$2,20), y el sobre de 5 postales 450 colones (US$0.79), la novedad es el álbum de pasta dura que tiene un precio de 4,500 colones (US$7.9).
¿Cuánto me va a costar llenar el álbum? Es la pregunta que los geeks futboleros nos hacemos en este momento. Bueno, el truco está en saber cuándo dejar de comprar sobres, dedicarse solamente a intercambiar y limitar la compra de postales sueltas hasta el puro final.
Matemáticamente el caso se conoce como El Problema del Coleccionista y ha sido ampliamente estudiado en probabilidad y matemática. En particular nos referiremos al Problema del Coleccionista con Extracciones de Grupos donde sacamos muestras con reemplazo de grupos equi-probables de un tamaño fijo m de una población finita S, o en español, compramos sobres de 5 postales cada vez que podemos hasta llenar el total de 670. Veamos cómo lograr que su presupuesto no se vea comprometido y lograr aun así la meta.

La mala estrategia, llenar el álbum a punta de comprar sobres
Cuando empezamos a comprar sobres la mayoría de las postales son nuevas, pero a medida que seguimos comprando empiezan a salir las repetidas. Wolfgang Stadje demuestra en “The collector´s problem with group drawings” que la probabilidad de llenar el álbum luego de haber comprado k sobres es:
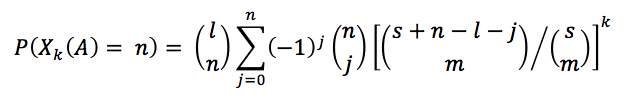
Tamaña formulita… Para nuestros efectos l=s=n = las 670 postales que nos separan de la gloria, m = 5 postales por paquete y k el número de paquetes que tendremos que comprar. P(Xk(A) = 670) es la probabilidad de obtener al menos un subconjunto que nos dé como resultado el álbum lleno. La ecuación se reduce entonces a:
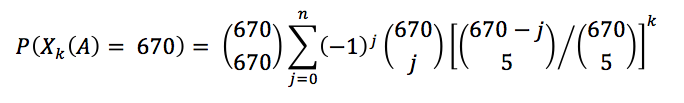
Y todavía hay gente que dice que para qué sirven las combinaciones…
Nos interesa el número k de paquetes que resulte en una probabilidad de 0.5 de llenar el álbum.
Este sencillo código en R (en realidad puede ser en cualquier lenguaje donde no haya que ponerse a hacer la fórmula de combinaciones desde cero) nos lleva al resultado que andamos buscando.
# Panini
# Probabilidad de llenar el álbum Panini dado un número de paquetes
# De acuerdo con la formula planteada por Wolfgang Stadje en
# The Collectors problem with Group Drawings
# Advances in Applied Probability Vol.22 No. 4 (Dec., 1990) pp 866 – 882
Postales <- 670
Enpaquete <- 5
Paquetes <- 920
Probabilidad <- 0
for(j in 0:Postales) {
Probabilidad <- Probabilidad + (-1)^j * (choose(Postales,j))*
(choose((Postales-j),Enpaquete)/choose(Postales,Enpaquete))^Paquetes
}
Probabilidad
Precisamente con 920 paquetes P(Xk(A) = 670) = 0.5 de llenar el álbum.
La persona más suertuda del mundo sería aquella que compre 670/5 = 134 paquetes y no tenga ni una postal repetida. Sin embargo, la ecuación no aguanta esa posibilidad. De hecho, no es sino hasta 634 paquetes que empezamos a tener posibilidades mínimas. En la siguiente tabla veamos las probabilidades según el número de paquetes en incrementos de 100 sobres, y lo más importante, veamos cuánto nos costaría cada estrategia.
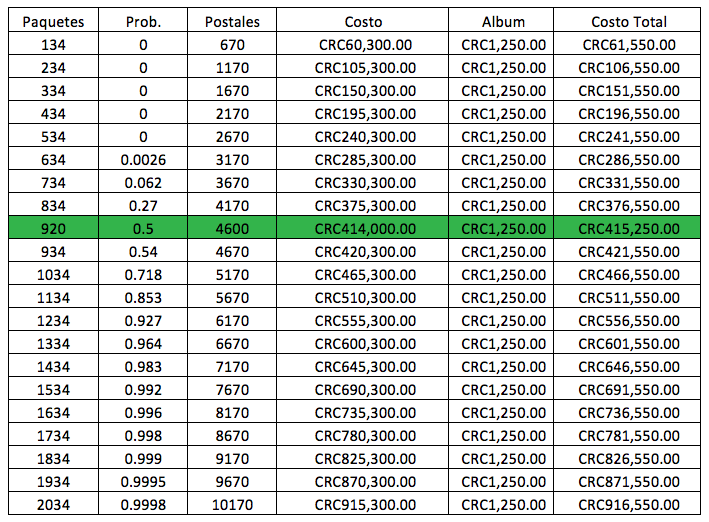
El costo promedio de completar todas las postales (más el álbum) es de 415,250 colones (US$728.50) mediante la estrategia de compra de paquetes. Y ojo que rapidito se va por encima de los US$1,000 si las últimas postales se niegan a aparecer.

¿Para qué son los amigos?
“La tengo, la tengo, no la tengo” suena en todos los idiomas en estos días. Sylvain Sardy junto con Yvan Velenik de la Section de mathématiques de la Université de Genève nos dan una buena estrategia en Paninimania: sticker rarity and cost-effective strategy. Primero, estos dos suizos, rivales de primera ronda de Costa Rica, demostraron para el mundial del 2014 que las postales siguen una distribución uniforme y que no hay Messis ni Cristiano Ronaldos con menos oferta. Cuando el “vivazo” en la Avenida Central les quiera vender a Neymar por cinco mil colones recuérdenle que sale igual que Nawaf Al-Abed de Arabia Saudita y que Kwak Taehwi de Korea del Sur. Sardy y Velenik además demostraron mediante simulación Monte Carlo como se van desvaneciendo las postales nuevas a mayor compra de sobres. Ajustando para Rusia 2018 el comportamiento es el siguiente:
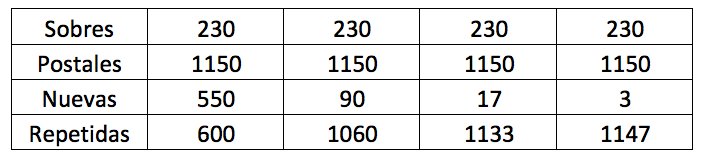
La tabla proviene de los 920 sobres promedio de la estrategia 1 y separados en 4 grupos iguales de 230 sobres. Los datos se basan en 12 cajas de 100 sobres cada una recolectadas en diferentes cantones de Suiza para un total de 6,000 postales físicas, más los resultados de 60 millones de postales simuladas.
Con 230 sobres comprados es hora de usar sus fortalezas como negociador y proceder a intercambiar con sus compañeros de trabajo, sus amigos del barrio y su sobrino de 9 años. Históricamente Panini ha puesto a disposición un servicio de venta de hasta 50 postales sueltas a un precio de 1.5 veces el precio en el paquete, solamente compre postales sueltas cuando le falten las últimas 50 o menos. Aun suponiendo un precio de 2X por postal suelta, el costo total de esta estrategia sería:
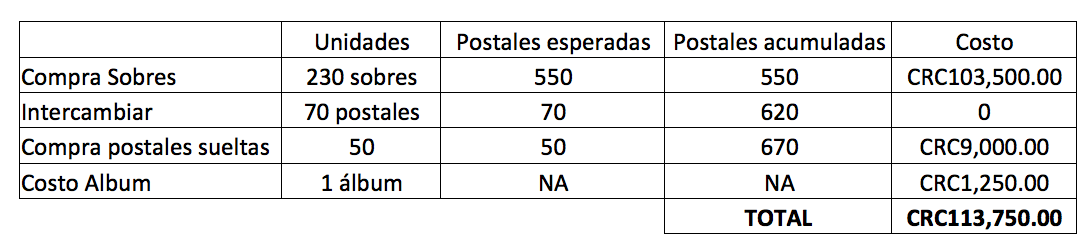
Tenga un grupo de unas 10 personas cercanas con quienes intercambiar postales.
Paciencia, calma y buen manejo de presupuesto
No se precipite, revise nuevamente la tabla 1, comprar sobres más allá de los 230 solamente harán que se gaste la prima de un carro nuevo y no llenará el álbum. No caiga en la Falacia del Apostador, pensar que como sólo le salen repetidas en el siguiente sobre vendrán las postales que le hacen falta. Si pasa pues así es doña Aleatoriedad, si no pasa recuerde que se lo advertí.
Hagamos un trato, yo voy a llevar mis estadísticas de número de sobres comprados, postales nuevas y postales repetidas. Compartamos y comparemos resultados al final del campeonato mundial a ver cómo nos fue con nuestras estrategias. Y sobre la compra sosegada, disciplinada, calmada y paciente de sobres… No prometo nada.
E!



