El Gráfico de Sumas Acumuladas, generalmente llamado CuSum está hecho para identificar cambios pequeños pero constantes en la variable que está siendo medida. Previo a la era de las computadoras se usaba popularmente un procedimiento complicado y poco confiable, conocido como Máscara V. Veremos la forma tabular que es más confiable y fácil de entender.
Ejemplo 1 de Gráfico Cusum
Los siguientes datos son tomados del Engineering Statistics Handbook del NIST, en la Sección 6.3.2.3 CuSum Control Charts cada dato representa un promedio de 4 mediciones:
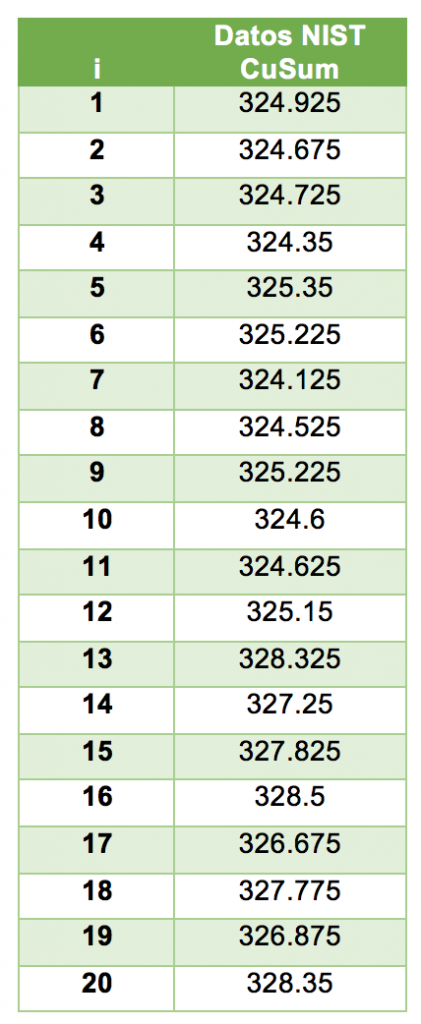
Tabla 1. Datos para gráfico CuSum de página del NIST (link indicado arriba)
Se desea establecer un gráfico CuSum con las siguientes características:
* NOTA: Se asume el valor de 0.635 como el error estándar de la media puesto que los valores son promedios de cuatro mediciones.
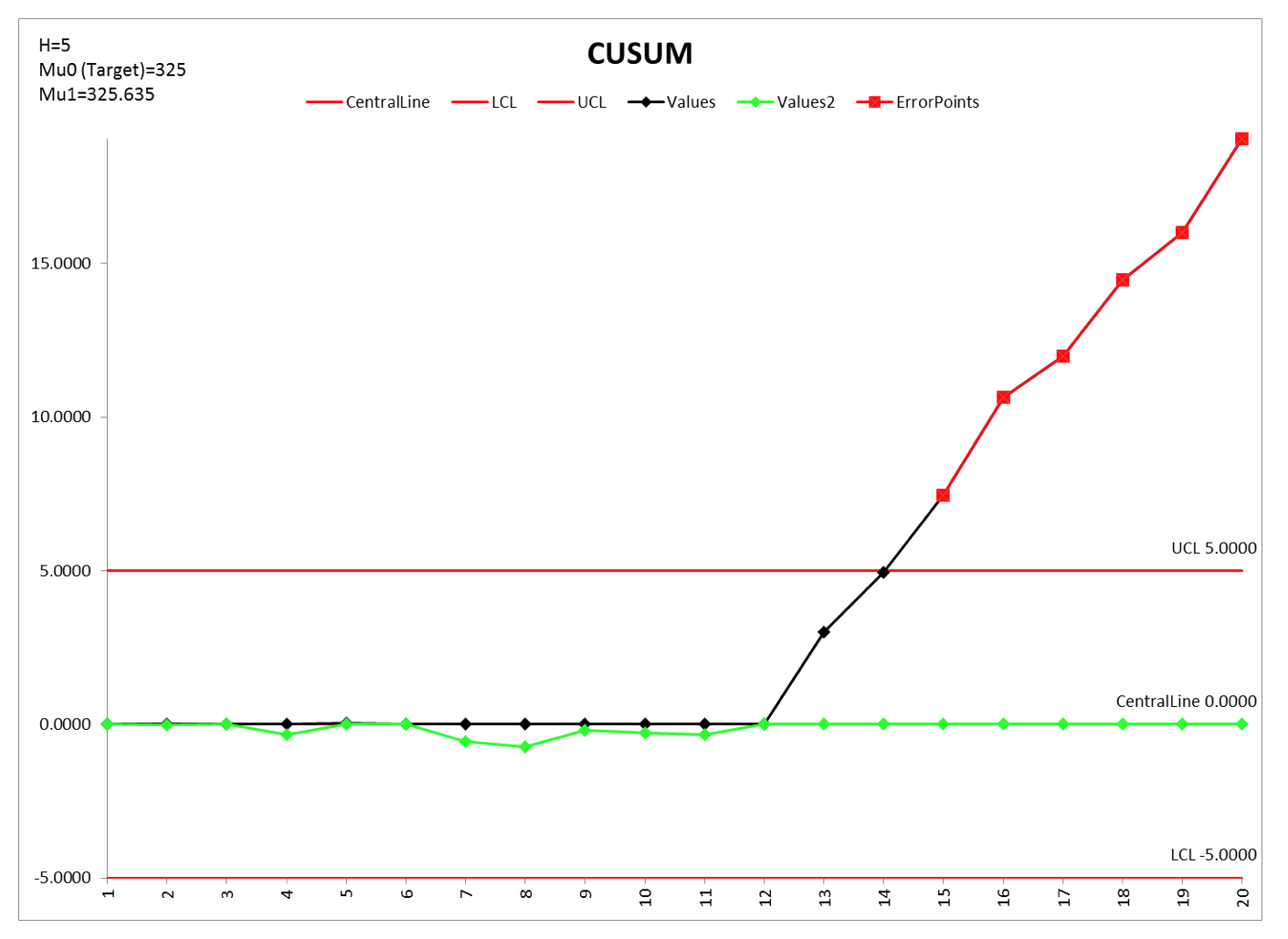
Gráfico 1. Gráfico de Control CuSum
El gráfico indica un estado de ausencia de control. Veamos los cálculos de los valores que componen el gráfico.
Cálculo de los valores Ejemplo 1.
El valor inicial C0 para iniciar los cálculos es:
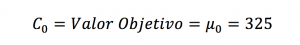
De ahí en adelante los valores a graficar se calculan mediante las fórmulas:
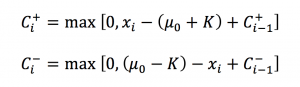
Donde:
Los valores iniciales de
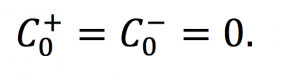
Tabla 2. Los tres primeros valores del Gráfico 1 CuSum
Puede confirmar el resto de los valores de Ci
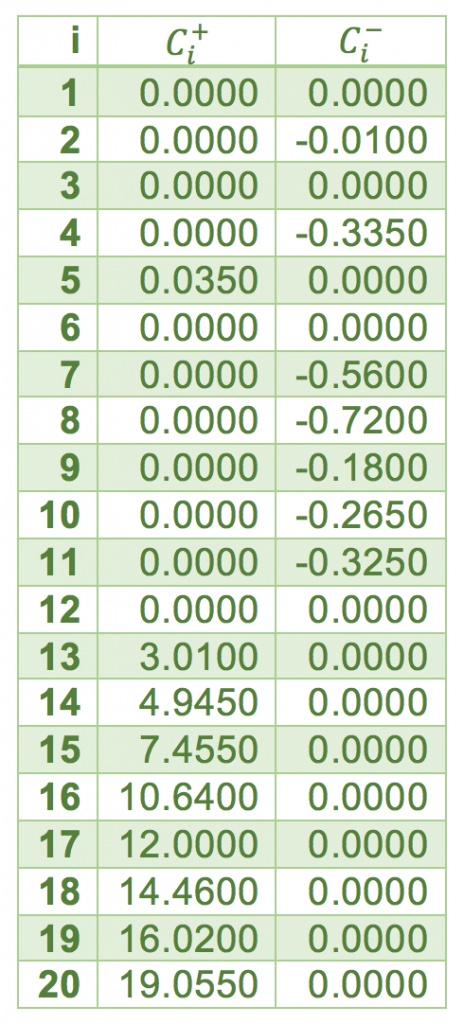
Tabla 3. Todos los valores del Gráfico 1 CuSum
NOTA: los valores de 
se toman negativos para que acumule hacia el lado de abajo del valor objetivo.
Ejemplo 2 cambio deliberado de la media
Al igual que hicimos con el gráfico EWMA vamos a usar los datos de Douglas Montgomery para demostrar un cambio pequeño en el proceso. De los siguientes 30 datos, los primeros 20 se obtuvieron de forma aleatoria de una distribución normal con media = 10 y desviación estándar = 1. Los siguientes 10 datos fueron tomados aleatoriamente de una distribución normal con media = 11 y desviación estándar = 1.
Los datos son los siguientes:
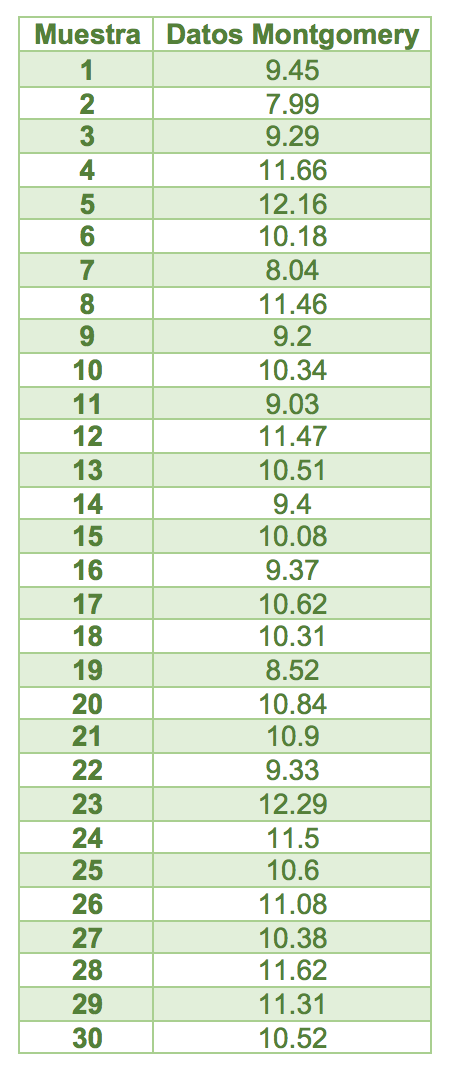
Tabla 5. Datos para Gráfico CuSum tomados de Introduction to Statistical Control de Douglas Montgomery
Vamos a hacer el gráfico CuSum con μ0=10, μ=1, y desviación estándar = 1. Estamos interesados en un cambio de la media de 1 desviación estándar, K = ½ puesto que la desviación estándar es 1, y H=5.
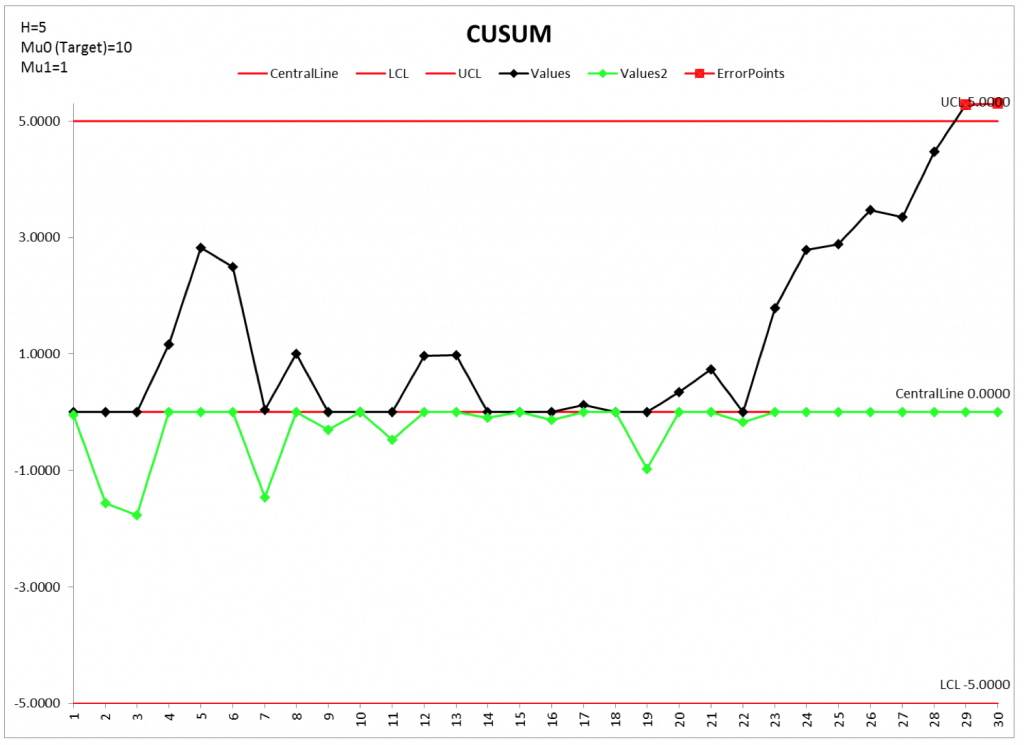
Gráfico 2. Gráfico de Control CuSum con estado fuera de control
En la muestra 29 se observa claramente un estado fuera de control. En las muestras precedentes ya se observaba una tendencia hacia arriba.
El gráfico CuSum detectó un cambio en el proceso en la muestra 29. Se invita al lector a probar ambos conjuntos de datos con gráficos tradicionales de Shewhart. Verá que no se detecta el cambio en el proceso con la regla de una muestra por encima o por debajo de los límites de control. Los gráficos de control especiales, aunque menos intuitivos que los gráficos tradicionales, verdaderamente detectan más rápido variaciones pequeñas que estén afectando al proceso.
