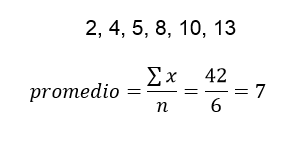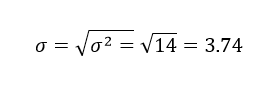Una pregunta frecuente en nuestros entrenamientos es ¿cómo se explica, o cómo se “ve” la desviación estándar? Lo interesante es que la pregunta no la están haciendo estudiantes de un curso de Estadística Básica, sino profesionales que utilizan está medida todos los días en reportes, investigaciones, validaciones, en fin, en la toma diaria de decisiones. El blog de hoy lo dedicaremos a este importante cálculo y sus implicaciones.
Ya anteriormente tocamos el tema de cómo hacer una estadística descriptiva efectiva, y también más recientemente nos referimos específicamente al promedio y los cuidados que debemos tener con su uso. La desviación estándar nos ayudará a contestar las preguntas ¿cuánto varían los datos alrededor del promedio? y ¿cuánto se extienden los datos a lo ancho? Como hemos indicado en otras ocasiones, las respuestas van a tener sentido cuando se comparan con algo (especificaciones, metas, niveles de servicio) y no por ellas mismas.
EL PROBLEMA DE EXPRESAR UNA MEDIDA DE LA VARIACIÓN Y LA SOLUCIÓN PARCIAL (DIFERENCIAS O RESIDUOS AL CUADRADO)
Si el promedio está bien calculado nos dará como resultado un valor que representa el balance, y no necesariamente el centro, de un conjunto de datos. Trataremos de seguido de promediar las diferencias alrededor de ese valor a partir del siguiente conjunto:
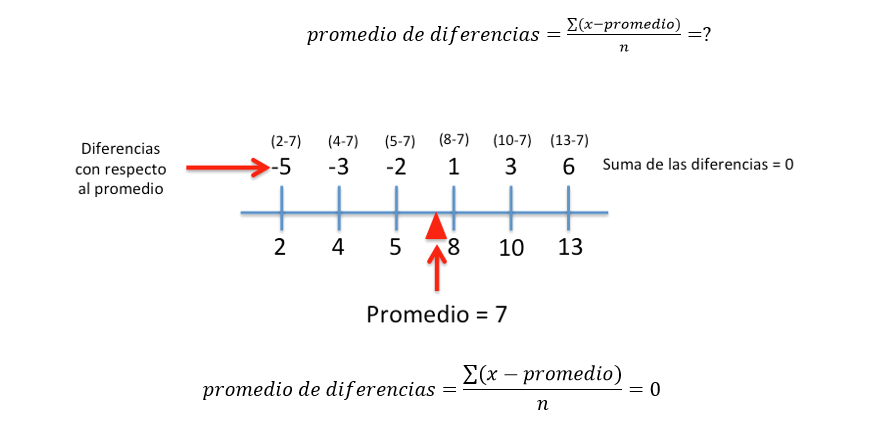
Estimación inicial del promedio de las diferencias:
La estimación de diferencias solamente nos permitirá verificar que el promedio está bien calculado pues la suma de las diferencias SIEMPRE será cero. Hay dos formas de resolver este problema, una sería sumar las diferencias absolutas, y la otra sumar las diferencias al cuadrado. Existen razones matemáticas para favorecer el uso de las diferencias cuadradas lo que nos lleva al cálculo que conocemos como Varianza.
La varianza es matemáticamente eficiente pero tiene dos problemas prácticos, los cálculos hacen que el número resultante no tenga relación con los datos y la unidad de medición original se pierde y termina expresándose al cuadrado. Por ejemplo si nuestra unidad de medida es kilogramos, la varianza está expresada en kilogramos cuadrados (que de paso no significa nada).
GRADOS DE LIBERTAD
Cuando se trabaja con toda la población el cálculo de la varianza se hace con N, o sea se incluye toda la población. Cuando se trabaja con muestras se hace un ajuste dividiendo entre “n-1” grados de libertad. Además se usan letras griegas para los valores poblacionales, y alfabeto “romano” para los cálculos muestrales.
Las respectivas fórmulas son las siguientes:
La manera más sencilla de definir “grados de libertad” es en términos de un hipotético experimento. Usted tiene “n” elementos en su muestra, ¿cuántos puede escoger aleatoriamente? La respuesta es n-1, pues el último no puede ser escogido al azar (sólo ese queda).
Una forma más matemática es indicar que cualquier suma de n-1 residuos (diferencias con respecto al promedio) determinará el valor del residuo faltante, pues como vimos anteriormente esta suma siempre será cero. Cuando estimamos los residuos a partir de “X barra” en lugar del valor poblacional μ “mu” debemos aplicar un grado de libertad para mantener la restricción de que la suma de residuos debe ser igual a cero, o dicho de otra manera restamos uno por el valor que estimamos (X barra).
CÓMO SE CONVIERTE LA VARIANZA EN UN VALOR PRÁCTICO
La varianza con toda su elegancia matemática no tiene significado práctico inmediato. La forma práctica de la estimación de la variación la da la desviación estándar, que simplemente requiere que le apliquemos raíz cuadrada a la varianza. Con este ajuste tendremos un valor numérico que podremos ver y explicar, y además, en las mismas unidades que los datos originales.
 Aplica nuevamente el concepto de grados de libertad.
Aplica nuevamente el concepto de grados de libertad.
Para los datos anteriores, asumiendo que se trata de una población la desviación estándar es:
EL TRUCO PARA “VER” LA DESVIACIÓN ESTÁNDAR
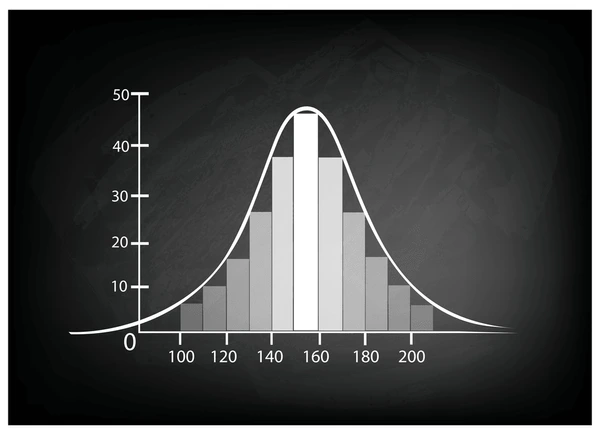
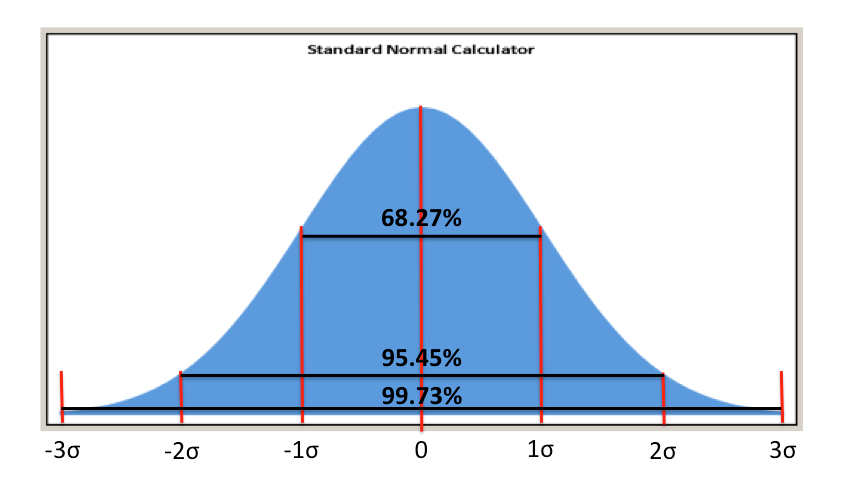
Asumiendo que los datos provienen de una distribución normal, podemos hacer la siguiente generalización:
Usted puede “dibujar” en su cabeza el “ancho” de la distribución sumando y restando 3 desviaciones estándar al promedio, luego puede compararlo con especificaciones o metas y determinar rápidamente el desempeño de su trabajo.
Para el ejemplo que hemos venido utilizando, asumiendo que se pueden dar valores negativos:
+/- 1 desviación estándar, 68.27% de la población, entre 3,26 y 10.74
+/- 2 desviaciones estándar, 95.45% de la población, entre -0.48 y 14,48
+/- 3 desviaciones estándar, 99.73% de la población, entre -4.22 y 18.22
Si lográramos disminuir la desviación estándar a la mitad en el mismo “ancho” tendríamos el famoso “6 sigma”, o sea, 6 desviaciones estándar a cada lado del centro.
El término “desviación estándar” lo uso por primera vez Karl Pearson en una conferencia en 1893, y aparece por primera vez en el paper “Contributions to the Mathematical Theory of Evolution” también de Pearson en 1894. El término substituyó a otros más complicados como “raíz media del error cuadrático”, “error cuadrado promedio” y “error medio”. El término “Varianza” fue usado por primera vez por Ronald Fisher en 1918 en uno de los documentos más importantes en la historia de la estadística: “The Correlation Between Relatives on the Supposition of Mendelian Inheritance”. Ambos documentos pueden ser encontrados en los respectivos links.