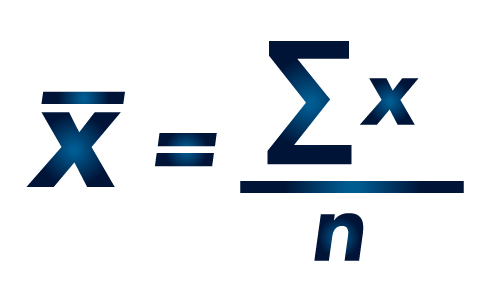Esta es la famosa fórmula del cálculo de la media aritmética:
Vamos a revisar algunas curiosidades de este venerable ícono de la estadística descriptiva.
Si preguntamos en la calle qué es el promedio las respuestas más comunes que obtendremos son “el centro”, o “lo que más se repite”. Desafortunadamente ninguna de estas respuestas identifica a la media. La primera se refiere a la mediana, y la segunda a la moda.
EL EFECTO DE VALORES EXTREMOS
Supongamos que una tienda de ropa de marca hace un estudio para decidir si abre una franquicia en la Ciudad de San Isidro del General, en el cantón de Pérez Zeledón.
Pérez Zeledón es un cantón al sur de la provincia de San José, Costa Rica. Se tomó una muestra de 32 salarios mensuales de trabajadores de esa zona. Los datos (en dólares) y su respectivo promedio se muestran a continuación:
|
1184.01 |
1561.43 | 1167.24 |
|
1237.95 |
1041 | 1590.96 |
|
991.47 |
899.49 | 1116.64 |
|
1084.5 |
1445.62 |
916.81 |
| 974.32 | 1405.66 |
1430.09 |
| 1566.49 | 1118.2 |
1264.32 |
|
1149.21 |
1317.36 |
1362.75 |
| 1543.69 | 1138.53 |
1298.73 |
|
1367.2 |
1224.71 | 1323.5 |
| 1301.47 | 1217.99 |
1335.02 |
| 1302.75 |
1511.92 |
El promedio de los salarios mensuales anteriores es: $1,262.22
De acuerdo con diferentes informes económicos este número se coloca en la parte baja de los ingresos de una familia de clase media en Costa Rica. La tienda “de marca” probablemente decidiría establecer una operación pequeña y ver cómo evoluciona (aunque recuerde que nunca se toma una decisión solamente con un promedio).
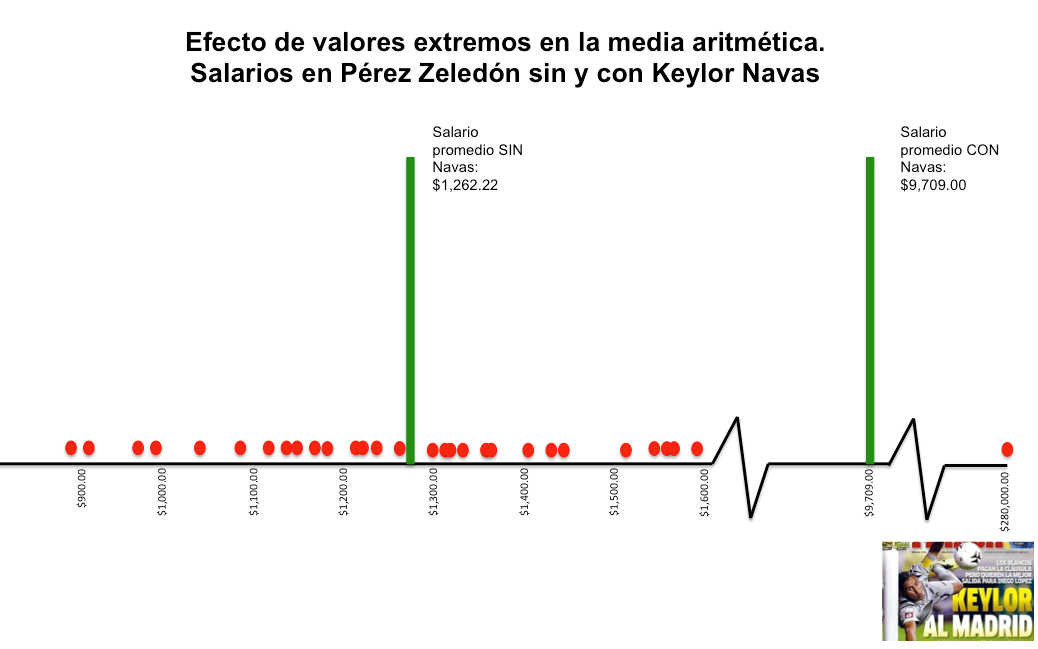
Supongamos ahora que en la muestra aleatoria se incluye a Keylor Navas quien acaba de ser contratado como el nuevo portero del Real Madrid, y además resulta que su ciudad natal es San Isidro del General. Su salario mensual durante los próximos seis años será de aproximadamente $280,000.00. Si incluimos el salario de Navas en el cálculo del promedio tendremos el siguiente resultado:
Salario promedio mensual: $9,709.00
Ese número colocaría a los habitantes de “Pérez” o PZ, como decimos los ticos, en el estrato de clase alta en cualquier país del mundo. La tienda abriría una franquicia igual, o más grande que su contraparte en Dubai o en New York. La decisión sería del todo incorrecta pues el resultado es una de las curiosidades (o problemas) de la media aritmética, cuando hay valores extremos la media se desplaza en la dirección de esos valores.
El salario estratosférico de nuestro “galáctico” es un dato espurio, o un “outlier”, que no se comporta como el resto de la muestra.
Note como en este “dot plot” tenemos que partir la escala dos veces, una para poder mostrar el salario promedio con el Efecto Keylor, y la otra para poder mostrar el punto que corresponde al salario de Navas.
El promedio NO es el centro, ni el 50%, es UN CÁLCULO que nos indica donde está el BALANCE de un conjunto de datos. Si los datos se comportan de acuerdo con la Distribución Normal entonces sí es el centro o el 50%. Además, cuando los datos son normales: media=mediana=moda. Pero cuando hay valores extremos el cálculo se desplazará hacia el lado de los extremos para poder mantener el balance.
EL FENÓMENO WILL ROGERS
William Penn Adair Rogers fue un cómico norteamericano conocido por su aguda sátira política.
Una frase suya se convirtió en una curiosidad estadística que además, tiene interesantes implicaciones prácticas. La frase dice lo siguiente:
“Cuando los pobres de Oklahoma se mudaron a California, elevaron el nivel de inteligencia de ambos estados”.
Rogers se refería específicamente a la gran migración de los años 1930s en la cual alrededor de un millón de “Okies” migraron a California. “Okie” era un nombre despectivo para referirse a los pobres y desplazados de Oklahoma. La frase original en inglés dice lo siguiente:
“When the Okies left Oklahoma and moved to California, they raised the average intelligence in both states”.
Piénselo un poco, ¿será esto posible?… Veamos cómo funciona.
Considere los siguientes conjuntos de datos:
A = {1,2,3,4,5}
B = {6,7,8,9,10}
PROMEDIO DE A = 3
PROMEDIO DE B = 8
Ahora pasemos el 6 y el 7 del Conjunto B al Conjunto A y calculemos de nuevo los promedios.
A1 = {1,2,3,4,5,6,7}
B1 = {8,9,10}
PROMEDIO DE A1 = 4
PROMEDIO DE B1 = 9
Efectivamente, aumentaron los promedios de ambos conjuntos.
En medicina la detección temprana de enfermedades, especialmente cáncer, produce precisamente este efecto. Se mejora la detección de la enfermedad, por lo tanto las personas enfermas dejan el grupo de personas sanas más rápido. Como consecuencia aumenta la esperanza de vida de los sanos. Pero como la detección se hizo mucho más temprano entonces también aumenta la vida promedio de las personas enfermas. Ambos grupos aumentan su promedio de vida. Se puede pensar erróneamente que nuevos tratamientos están dando mejores resultados cuando en realidad la causalidad viene de la detección temprana. El nombre técnico es Migración de Estado.
El Efecto de los Valores Extremos y el Fenómeno Will Rogers muestran claramente las limitaciones de la media aritmética como elemento para la toma de decisiones. Nunca tome una decisión con un promedio, haga una estadística descriptiva completa que contemple varias medidas de tendencia central, medidas de dispersión y formas gráficas, y sobre todo incluya alguna forma de comparación (contra especificaciones, estándares, o metas).