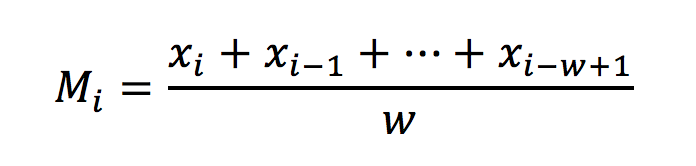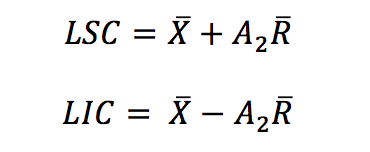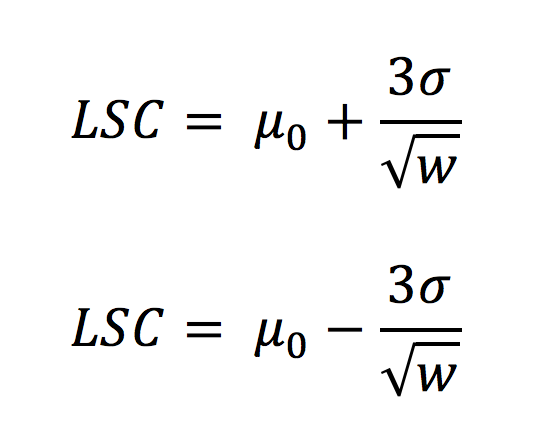GRÁFICOS DE CONTROL PARA SITUACIONES ESPECIALES (parte 1 de 3)
Iniciamos hoy una pequeña serie sobre algunos de los gráficos de control especiales. Los gráficos de control de Shewhart, para variables y para atributos, funcionan bien como instrumentos para detectar variación especial en la mayoría de los casos, algunas veces se requiere de gráficos alternativos para situaciones inusuales. Nuestro e-book sobre las siete herramientas de la calidad es una buena referencia para empezar a conocer los gráficos de control (7 Herramientas de la Calidad).
La siguiente es la lista de gráficos especiales que cubriremos en esta serie.
| Gráfico | Se usa para |
| Gráfico de promedio móvil | Detectar cambios de variación de los procesos menores a 1.5 desviaciones estándar.
Muy útil para procesos continuos. Más sencillo de calcular que otros gráficos para detección de cambios pequeños en la variación. |
| Gráfico EWMA | Detectar cambios en la variación de los procesos menores a 1.5 desviaciones estándar. Se basa en datos históricos y no solamente en la última muestra recolectada. Permite al analista planear con anticipación si quiere más atención a los datos históricos o a los datos más recientes. |
| Gráfico CUSUM | Detectar cambios en la variación de los procesos menores a 1.5 desviaciones estándar. Una vez definida una meta, el gráfico monitorea desviaciones de esa meta y ayuda a detectar cambios pequeños (entre 0.5 y 1 sigma). |
| Gráfico G | Situaciones que ocurren raramente (muy baja frecuencia o mucho tiempo entre ocurrencias).
NOTA: Puede encontrar información sobre el gráfico G en estas dos referencias. |
Empecemos entonces esta serie con el gráfico de promedio móvil.
Gráfico de promedio móvil
| Nombre: | Gráfico de Promedio Móvil | ||||||||||||||
| Usos: | · Para datos continuos.
· Para detectar cambios pequeños en la variación. · Para procesos continuos (procesos químicos, procesos de industria alimentaria, entre otros). · Cuando solamente hay una muestra por período. |
||||||||||||||
| Promedio móvil (el dato que se grafica) | Se determina el promedio de las w unidades que se agrupan. Para cada período i se elimina el dato más viejo de los w datos agrupados. El promedio móvil se calcula:
|
||||||||||||||
| Límites de control (Forma 1) * | Calcular los límites basados en las constantes tradicionales de Shewhart para tamaños de muestra w.
Línea de Centro = promedio de todos los datos en estudio
Donde: X es el promedio de todos los valores en estudio. A2 es una constante que depende del tamaño de w.
Los valore más comunes de A2 son:
* La Forma 1 fue propuesta por Grant y Leavenworth en el libro: Statistical Quality Control. |
| Límites de control (Forma 2) ** | Utilizar un centro objetivo (target value).
Calcular la desviación estándar de los datos en estudio, o conseguir una desviación estándar histórica.
Línea de centro: valor objetivo.
Donde: es el valor objetivo. es el valor de la desviación estándar. w es el número de unidades que se usan en el promedio móvil.
NOTA: la Forma 2 la propone Douglas Montgomery en su libro Introduction to Statistical Quality Control. |
Ejemplo del cálculo del Promedio Móvil
Una planta hace un análisis diario para determinar el porcentaje de cierto químico en su material prima, producto en proceso y producto terminado. El efecto suavizador del gráfico es similar a lo que le pasa cuando se agregan mezclan y/o se licúan componentes en un proceso de producción continuo. Los datos de los primeros 10 días de producción se muestran a continuación:
| Promedio | Promedio móvil | ||
| Fecha | Valor diario | móvil 3 días | corresponde a: |
| 1-Sep | 0.24 | ||
| 2-Sep | 0.13 | ||
| 3-Sep | 0.11 | 0.160 | Promedio primeros 3 días |
| 4-Sep | 0.19 | 0.143 | Promedio días 2, 3 y 4 |
| 5-Sep | 0.16 | 0.153 | Promedio días 3, 4 y 5 |
| 6-Sep | 0.17 | 0.173 | Promedio días 4, 5 y 6 |
| 7-Sep | 0.13 | 0.153 | Promedio días 5, 6 y 7 |
| 8-Sep | 0.17 | 0.157 | Promedio días 6, 7 y 8 |
| 9-Sep | 0.10 | 0.133 | Promedio días 7, 8 y 9 |
| 10-Sep | 0.14 | 0.137 | Promedio días 8, 9 y 10 |
Tabla 1. Porcentaje de CaO sin reaccionar
en la etapa intermedia de un proceso químico.
Statistical Quality Control. Grant y Leavenworth.
Observe cómo el promedio móvil de 3 valores se calcula a partir del tercer día. En el cuarto día el promedio móvil corresponde a los días 2, 3 y 4, se “bota” el dato más antiguo de la serie de tres datos y se agrega el más nuevo. El día 5, se elimina el dato del día 2 y se agrega el dato del día 5, y así sucesivamente.
Vamos a completar el set de datos y hacer el gráfico de promedio móvil.
| Promedio | ||
| Fecha | Valor diario | móvil 3 días |
| 1-Sep | 0.24 | |
| 2-Sep | 0.13 | |
| 3-Sep | 0.11 | 0.160 |
| 4-Sep | 0.19 | 0.143 |
| 5-Sep | 0.16 | 0.153 |
| 6-Sep | 0.17 | 0.173 |
| 7-Sep | 0.13 | 0.153 |
| 8-Sep | 0.17 | 0.157 |
| 9-Sep | 0.10 | 0.133 |
| 10-Sep | 0.14 | 0.137 |
| 11-Sep | 0.16 | 0.133 |
| 12-Sep | 0.14 | 0.147 |
| 13-Sep | 0.17 | 0.157 |
| 14-Sep | 0.15 | 0.153 |
| 15-Sep | 0.20 | 0.173 |
| 16-Sep | 0.26 | 0.203 |
| 17-Sep | 0.16 | 0.207 |
| 18-Sep | 0.00 | 0.140 |
| 19-Sep | 0.18 | 0.113 |
| 20-Sep | 0.18 | 0.120 |
| 21-Sep | 0.20 | 0.187 |
| 22-Sep | 0.11 | 0.163 |
| 23-Sep | 0.30 | 0.203 |
| 24-Sep | 0.21 | 0.207 |
| 25-Sep | 0.11 | 0.207 |
| 26-Sep | 0.17 | 0.163 |
| 27-Sep | 0.18 | 0.153 |
| 28-Sep | 0.13 | 0.160 |
| 29-Sep | 0.28 | 0.197 |
| 30-Sep | 0.16 | 0.190 |
| 1-Oct | 0.14 | 0.193 |
| 2-Oct | 0.16 | 0.153 |
| 3-Oct | 0.14 | 0.147 |
| 4-Oct | 0.10 | 0.133 |
| 5-Oct | 0.13 | 0.123 |
| 6-Oct | 0.20 | 0.143 |
| 7-Oct | 0.14 | 0.157 |
| 8-Oct | 0.10 | 0.147 |
| 9-Oct | 0.18 | 0.140 |
| 10-Oct | 0.11 | 0.130 |
Tabla 2. Porcentaje de CaO sin reaccionar
en la etapa intermedia de un proceso químico. Datos completos
Statistical Quality Control. Grant y Leavenworth.
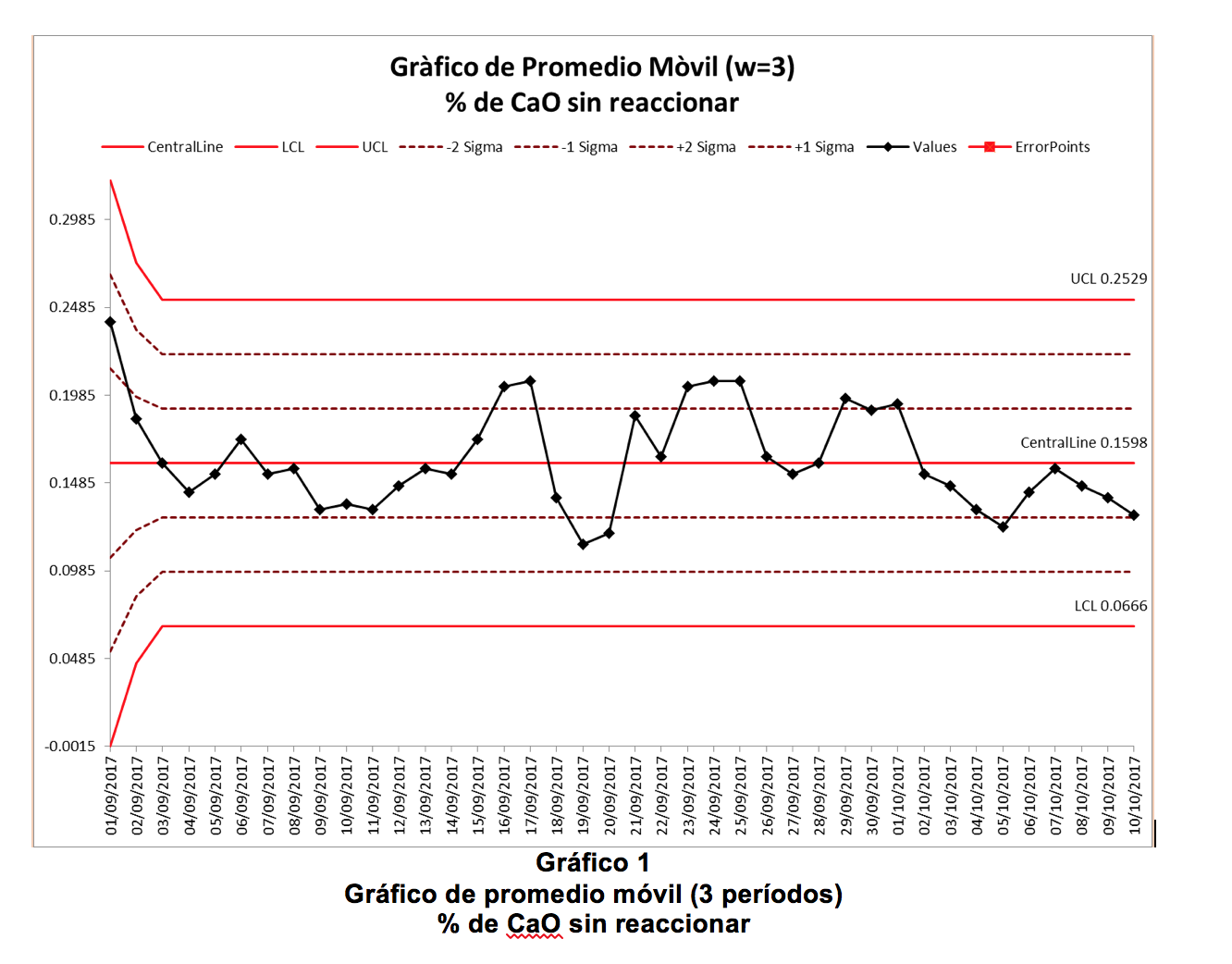
Los primeros dos cálculos de los límites se hacen con w=1 y w=2, por eso son más anchos que el resto. Además, en el primer promedio móvil solamente hay un dato, mientras que el segundo es el promedio de los dos primeros datos. Del tercero en adelante los límites se estabilizan con w=3 períodos.
El gráfico de promedio móvil da una mejor idea del comportamiento del porcentaje sin reaccionar de CaO que un gráfico de puntos individuales.
Conocer los usos específicos de los diferentes gráficos de control (tradicionales o especiales) permite un mejor análisis del comportamiento de la variación en los procesos. Continuaremos en la siguiente ocasión con el gráfico EWMA, digamos por ahora que es un promedio móvil con esteroides.