La versión web del Noticiario Informe 11 del día 21 de enero de 2018 publica el titular “Guerra de Encuestas” a raíz de la publicación por parte de varias empresas durante los últimos días de diferentes resultados de encuestas de intención política sobre las elecciones que se avecinan. Sin embargo, la pregunta que tal vez usted tenga y que también mi persona pensó fue, ¿Qué tan confiables son las mismas? Con solo revisar un poco los resultados publicados llama la atención que difieren en un grado importante unas de otras.
El tema de las encuestas políticas en nuestro país no es nuevo, siempre en cada elección previamente unas semanas antes al día decisivo recibimos este tipo de noticias, con el fin de crear opinión y adelantar lo que pueda ser el resultado final. Ahora bien, lo anterior puede ser el fin noble por así decirlo, pero también se ha conocido en elecciones anteriores de la duda razonable que algunas de estas encuestas puedan tener y la forma en que se calcularon, en especial algunas encuestas para la Elección del 2014, donde daban por un hecho la victoria del candidato de Liberación Nacional Johnny Araya cuando al final el vencedor fue el actual presidente Luis Guillermo Solís del Pac. Esto hizo pensar a la opinión publica en general de la dudosa calidad de los resultados de las encuestas y algunas otras “cosillas” que no vienen al caso comentar (imagínese el emoticón con cara pensativa aquí jajaja).
En primera línea hay que dejar claro, las encuestas estadísticas son un excelente recurso investigativo, que si es aplicado con una adecuada base metodológica puede generar resultados de una gran calidad, sin embargo, recuerde al Tío Ben de Spiderman 1 (sí, el del actor Tobey Maguire) cuando decía: ante un gran poder hay una gran responsabilidad… y es precisamente aquí donde aplicamos eso, realizar encuestas es un asunto de gran responsabilidad dado que, los resultados influenciaran en gran medida las acciones de las personas interesadas.
Pero pasemos a hacer un poco de análisis mas técnico, de ese en el que PXS nos encanta enseñar. Primero recordaremos que las encuestas son una herramienta de la estadística inferencial, pues se basan en el calculo de un tamaño de muestra que permite realizar inferencias sobre un comportamiento de una población, en este caso Costa Rica y su población de adultos, que son los que votan. Al ser estos instrumentos de inferencia, como usted sabe, implican un nivel de confianza y un error experimental que sumados, van a representar el famoso “margen de error”. ¿Qué es el margen de error? Pues muy sencillo, es un porcentaje de variación que puede tener cada resultado de la encuesta, el cual puede incrementar o decrementar el resultado y como es lógico pensar, lo que queremos es que este margen de error sea lo mas pequeño posible con el fin de garantizar la confiabilidad del resultado. Analicemos entonces como podemos calcular el tamaño de muestra para poder entender más en detalle el famoso margen de error que sale en las encuestas, esta ecuación es una de las más comunes utilizadas en estadística y es la que vamos a utilizar para explicarnos en detalle:
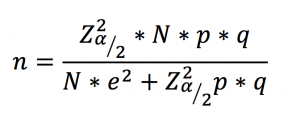
Como puede observar la ecuación anterior, hay varios componentes importantes, lo que queremos es definir “n”, dado que es la cantidad de personas que quiero encuestar para garantizar que puedo conocer la intención de voto, mmm, de nada mas y nada menos que un país. Aquí es donde pensamos, ¿Franklin dice que quiere saber cuántas personas debe encuestar para pronosticar la intención de voto por alguno de los candidatos actuales? Posiblemente nuestro pensamiento intuitivo es, debería ser un montón de gente, estamos hablando de un país de casi 5 millones de personas verdad… sin embargo, es interesante ver que no es tan así… Algunas consideraciones que debemos tomar en cuenta son:
- No son casi 5 millones los que debemos preguntarles, solamente debemos encuestar al estrato poblacional con edad igual o superior a los 18 años, eso descarta entonces a los niños y niñas del País. Según datos del TSE para diciembre de 2016 la cantidad de personas inscritas en el padrón nacional para votar fue de 3 256 590 personas, voy a usar ese dato como N de Población en mi formula, teniendo en cuenta el bajo ritmo de crecimiento poblacional y la tasa de decesos estimada del país (simplifico 😉)
- El Nivel de Confianza , que es un valor de un estadístico de la distribución Normal que me permite garantizar la confiabilidad de que lo buscado en la muestra realmente represente lo existente en la población, en este caso definimos una típica confianza de 95%, eso implica que la significancia, que es la probabilidad de que la muestra no muestre lo que esta en la población seria de 100% menos 95%, o sea 5%, más adelante vera que la subiré a 99% para hacer el estudio aún más confiable.
- El Error experimental se diferencia de la significancia en que se atribuye a la probable ocurrencia de efectos aleatorios naturales a cualquier estudio inferencial, o hablándolo a lo tico… es el chance de que cualquier cosa al azar nos afecte el estudio por efectos de Tatica Dios.
- Si sumamos el resultado de 100% menos la Confianza, o sea la significancia, al Error experimental tendremos nuestro margen de error de encuesta, algo así como:
Nivel de Significancia + Error Experimental = Margen de ERROR
El problema aquí ahora va a ser, en la ecuación el parámetro que se llama “p”. Esa “p” no es nada mas y nada menos que una probabilidad, es la probabilidad de comportamiento histórico de la característica buscada en el estudio estadístico (¿y aquí usted se vuelve a preguntar, de qué está hablando Franklin otra vez?).
La “p” o probabilidad de éxito es un concepto que se deriva de las distribuciones de probabilidad, en especifico de la binomial, donde vemos que buscamos saber si un resultado pasa o no pasa. Para los estudios políticos es algo mas complejo, pero podemos simplificar el asunto viendo que tiene ciertamente un evento binomial el preguntar ¿va usted a votar por este candidato? ¿Si o no? El votar por ende es totalmente un evento binomial, solo que aquí debemos hacer esta pregunta para todos los demás candidatos inscritos…. Analicemos una peculiaridad de nuestra elección, el caso Otto Guevara, queremos calcular nuestra “p” o probabilidad histórica de intención de voto, en este caso del Sr Guevara. Como usted sabe Otto se ha postulado de candidato en 4 elecciones consecutivas (si, que cansado, lo mismo opino). En el caso de Otto es fácil calcular la “p” que necesito en la ecuación, dado que tengo 4 elecciones donde he sabido históricamente cuanta gente del total de cada padrón electoral ha botado por él, por lo que debería sumar los padrones de cada una de las elecciones y sumar los votantes por el Sr Guevara en esas 4 elecciones y sabría mi “p”. Veamos un poquito de estadística descriptiva, los datos son cortesía del TSE y Wikipedia:
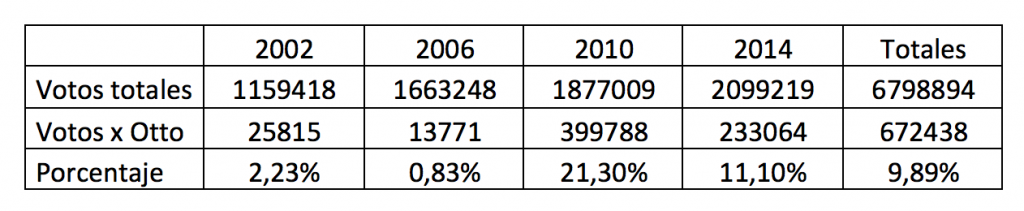
Como usted puede observar a Otto le fue mejor en la Elección de 2010, donde fue cuando llego a su pico más alto de votantes con 399 788 personas, un nada despreciable 21.30%, en las elecciones de 2014 bajo significativamente a 11,10%. Tomando en consideración esto, sumemos padrones y votos por Otto y saquemos una relación porcentual, que es 9,89%, este numero será la “p” o probabilidad de éxito que usaremos para Otto en específico. El otro dato, “q” que es la probabilidad de fracaso como se imaginará, es el complemento de “p”, o sea poquito más de 90% que no votaron por Otto (que montón jejeje).
¿Pero cómo hacemos con los otros candidatos? ¿Y sí, son un montón y además…como hacemos con los que son nuevos candidatos de paquete? Podemos hacer dos cosas, o seguir el mismo ejercicio para los candidatos que repiten, a semejanza de Otto o utilizar un viejo truco que se ha utilizado en Estadística y que la mayoría no sabe explicar de donde viene, la famosa “p” seteada en 0,5 o 50% (y si p es 50% “q” por ende es también 50%). El truco de setear “p” en 50% generalmente lo aprendemos en la universidad por recomendación de nuestros profesores cuando usted no conoce para nada el comportamiento histórico de la probabilidad de éxito, sin embargo, no se trata de aquel dicho que es mejor una mentira que te haga feliz que una verdad que haga lo contrario, por lo que explicaremos el por qué hacer esto. Hemos de decir que, si una población tiene efectivamente un comportamiento de una distribución binomial, los eventos binomiales son todos aquellos que son del tipo si o no, pasa no pasa, cumple o no cumple, muy similar como lanzar una moneda, donde sale escudo o corona; si es así, imagínese entonces que lo ideal es que salga un resultado la mitad de veces si y la mitad de veces no, o sea 50% y 50%, y voila! Esa es la razón de poner cuando uno no sabe la p en 50%; sin embargo, sepa algo de este viejo truco, hacer “p” este valor implicará que sus muestras tenderán a ser grandes, muy grandes; si usted puede calcular p de una forma aproximada como con nuestro amigo Otto, es mejor porque las muestras le tenderán a ser mas pequeñas, al final, la moraleja es, no sea perezoso dejando p en 50% (es broma).
Bueno, vamos de nuevo a los números, como es difícil tener una p por cada candidato que hay, y queremos saber de que tamaño debe ser la encuesta que aplicar, vamos a aplicar algunas simplificaciones, que son igual de validas mientras sean bien aplicadas. Vamos a sacar probabilidades de éxito, o sea “p´s” por partido político de los principales, y a los otros partidos que sacaron un quinto lugar o inferior en las elecciones de 2002, 2006, 2010 y 2014 vamos a darle una p de “otros” con base a la diferencia entre la suma de los votantes totales de las 4 elecciones menos los votantes de los 4 primeros lugares de las 4 elecciones en consideración, por lo tanto, tendríamos:
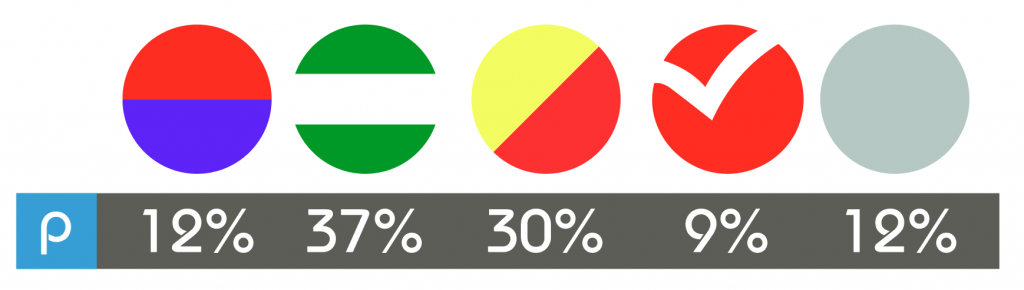
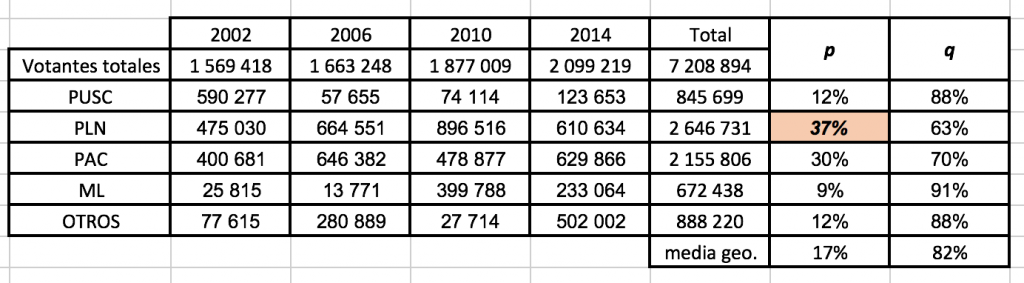
Fuente: Wikipedia y TSE
Como podemos ver, obtuve p´s de los partidos PUSC, PLN, PAC y ML respectivamente, que han sido los partidos más regulares en las ultimas elecciones. También saqué una p de “otros” de un 12% para agrupar los otros partidos políticos más allá del quinto lugar de resultados. Por lo que si quisiera sacar el tamaño de muestra para cada partido lo podría hacer, solo usando la p respectiva. Pero como lo que quiero es una “p” conjunta para todos, podemos hacer dos cosas, o la primera, lo simplifico y uso la “p” más grande de todos, en este caso la de Liberación Nacional, con un 37% o puedo sacar una p conjunta a través de la media geométrica (recuerde que no es de gente Cristiana, y sobre todo que pasó por el Greenbelt de Franklin promediar a lo salvaje porcentajes, si usted va a promediar porcentajes debe usar nuestra amiga la media geométrica). Teniendo eso en cuenta, nuestra “p conjunta” seria de 17%, que es más pequeña que el 37% mayor del PLN. Pros y contras, si usamos p en 37% vamos a garantizar mejores resultados, porque aumenta la confianza de los otros partidos y respeta el máximo comportamiento, aunque si usamos la p promedio de 17% tendríamos menor cantidad de muestra y por ende menos trabajo, mi consejo, analice las dos opciones y si puede utilice la p mayor; Yo voy a calcular los dos casos, veamos:
Con la p de 37%:
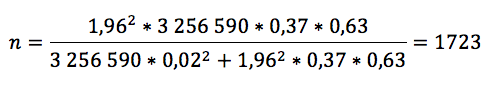
Con la p en 17%:
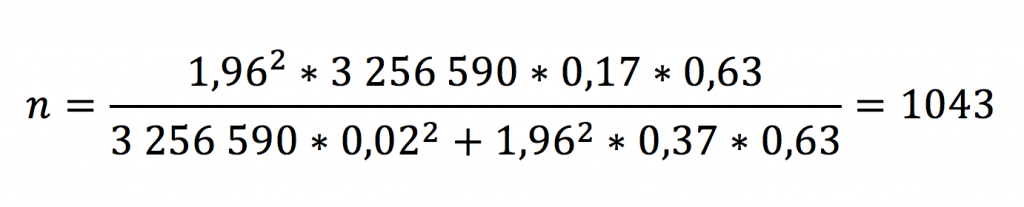
Como puede apreciar, la cantidad de personas que tenemos que encuestar para garantizar un margen de error de 3% (2% del Error experimental y 1% del nivel de significancia) es de 1723 personas, sobre una población de 3 256 590 personas, nada mal tomando en cuenta el gran tamaño de la población. También mire que con la p en 17% bajamos a 1043 personas, lo cual podría ser bueno para asuntos económicos pero arriesgado para términos de confiabilidad.
En todo caso solo calcular la muestra no es suficiente, también debemos garantizar algunas otras condiciones necesarias para el estudio, siendo estas las siguientes:
- Debemos garantizar aleatoriedad en la selección de los encuestados, debemos tomar en cuenta consideraciones de densidad demográfica, como por ejemplo que vive mas gente en la zona metropolitana o GAM que en la zona rural. En la elección donde Oscar Arias ganó a Otton Solís, Otton ganó por un amplio margen en la GAM, pero en el resto del país y sobre todo en las zonas rurales Oscar Arias ganó avallasadoramente, por lo que días antes de la elección casi ninguna encuesta acertó y según cuenta la leyenda urbana, fue por lo mal que se seleccionó la muestra.
- También, el método de aplicación de la encuesta cuenta. Las empresas encuestadoras por facilidad prefieren usar el alcance telefónico, sin embargo, este tiene la limitante de que la gente en veces no gusta contestar estas llamadas y con esto se tiende a sesgar la muestra. En otras empresas en ocasiones se encuesta personalmente, frente a frente con encuestadores sin embargo el problema de este método son principalmente los lugares donde se aplica la encuesta, tipo parques y centro comerciales lo que hace que factores tales como horarios y tipos de unidades muestrales también generen un sesgo sobre el estudio, al final es muy difícil que lleguen a su oficina a hacerle una encuesta de este tipo o no?
- Las empresas de encuestas “venden” estos estudios con base al margen de error, a menor margen de error el estudio implica un tamaño de muestra mayor, lo que lo hace más caro. Los partidos políticos y los periódicos o medios televisivos tal vez quieran ahorrar unos tantos millones de colones aumentando el margen de error, sin embargo, esto afectara posiblemente.
- Los candidatos que tengan resultados similares con más menos el margen de error técnicamente se podría decir que están empatados, por ejemplo, imagine que Juan Diego tenga un 16% de intención de voto y Álvarez Desanti un 18%. Aunque Álvarez tenga más si sumamos el margen de error en 4% a ambos resultados tendríamos a Álvarez entre 22% y 14% y a Juan Diego entre 20% y 12%, por lo que el intervalo de 20% a 14% es común a ambos, por lo que eso es lo que técnicamente le decimos un empate probable, y para dilucidar quién estará mejor habría que aumentar el tamaño de muestra para disminuir el margen de error.
Finalmente, también y aunque no sea algo que se haya comprobado, o por lo menos mi persona lo sepa, las encuestas pueden también ser manipuladas, algunas veces con fines no muy loables y otras con fines de manipulación de la opinión pública.
Las encuestas son una gran herramienta de la estadística, y si son usadas correctamente pueden ayudar a tomar decisiones muy importantes, incluso las del destino de un país. Suerte en su selección y que gane el mejor candidato, por el bien de Costa Rica.


