No sé ustedes, pero a mí me costó sangre entender cuál era la mano derecha y cuál era la mano izquierda. En serio, una herida y posterior cicatriz a los 5 o 6 años de edad finalmente me dio un mnemónico visual para entender la diferencia (la de la cicatriz es la izquierda)… y eso que soy zurdo.
Siempre es difícil recordar esos estados binarios totalmente contrarios, igual pasa con las puertas que indican “pull” o “push” (quién no ha pasado por la pena de ejecutar la acción contraria), y se complica más en casos más complejos como cuando tenemos que recordar cuál de los dos lados del cerebro es más pícaro y cuál el más ordenado (cerebro derecho: creatividad; cerebro izquierdo: orden).
Pero nada se compara con la dificultad de recordar los errores estadísticos, “brillantemente” llamados Error Tipo I, y Error Tipo II (y por supuesto, sus correspondientes probabilidades “alfa” α y “beta” β). Recuerdo que inclusive siendo profesor de Estadística en el Instituto Tecnológico de Costa Rica tenía que hacer un esfuerzo para relacionar correctamente ambos errores.
Siempre que tomemos una decisión en inferencia estadística, a partir de una muestra, nuestra decisión contará con la presencia invisible de los potenciales errores estadísticos. En términos prácticos “Rechazar lo bueno” – Tipo I y “Aceptar lo Malo” – Tipo II.
Vamos a ponerlo en una matriz que nos vaya ayudando a encontrar el mnemónico que andamos buscando.
Ahora veamos la misma matriz con el ejemplo que ha hecho a muchas personas entender y recordar los términos correctos.
Error Tipo I, la muchacha, la joven, la princesa, como usted la quiera llamar NO le abre la puerta al Príncipe Azul. Apréndase solamente esa relación y todas las demás le van a salir de forma muy sencilla. No abrirle, dejarlo ir, ignorarlo, cómo usted quiera recordarlo. Fácilmente vamos a completar la matriz de la siguiente forma: Si la muchacha le abre al príncipe la decisión es la correcta. Y por el otro lado, si la puerta la toca un sapo (que seguirá siendo sapo aún después del mítico beso de los cuentos de fantasía), o un monstruo, un ogro, Lord Voldemort, Freddy Krueger, etc. y nuestra heroína le abre, estará cometiendo el Error Tipo II, y si no le abre estará tomando la decisión correcta.
Garantizado que ya no se va a olvidar. Pongámoslo en una situación más de empresa con la siguiente matriz.
La escogencia del nuevo material a partir del análisis de una muestra es un asunto de mucho cuidado.
Habiendo explicado cómo entender los errores vamos a completar ahora el cuadro con la introducción del contraste de hipótesis y la escogencia de los valores de α y β.
CONTRASTE DE HIPÓTESIS
Sir Ronald Fisher fue el primero en utilizar, en 1935, el término “Hipótesis Nula”. El nombre implica “anular”, “nulificar” el objetivo del análisis. En términos prácticos significa “aquí no ha pasado nada”, “todo es igual que antes”, pero sobre todo “no se pudo demostrar ningún cambio, el estudio es nulo”. Pearson, contemporáneo, coterráneo (ambos ingleses), y adversario a muerte, lo complementó casi paralelamente con el concepto de Hipótesis Alternativa, “se demuestra que algo cambió”, “algo es diferente”.
Acercándonos a su forma matemática la Hipótesis Nula se denomina Ho (“Hache sub cero”) y la Hipótesis Alternativa H1 (“Hache sub 1”).
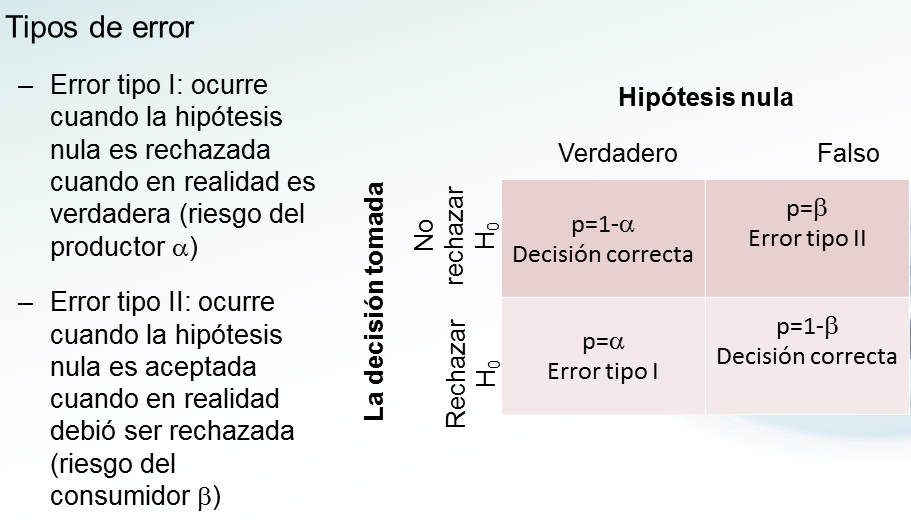
La forma estadística final y evolucionada de nuestra matriz, considerando el contraste de hipótesis, es la siguiente.
Si ha venido siguiendo toda la historia, encontrará muy sencillo traducir esta jerga matemática a nuestros ejemplos previos, príncipes y villanos incluidos.
Todavía nos falta definir los valores de los errores estadísticos, pero lo vamos a dejar para la próxima semana en una segunda parte. Por ahora solamente digamos que existe una relación entre el valor de alfa y la Selección de Futbol de México cuando juega en el Estadio Azteca (NOTA: conocimiento futbolístico previo es importante).
Recuerde el mnemónico: Error Tipo I, la princesa que dejó ir al príncipe azul.