¿Cómo darle seguimiento, y de paso encontrar algún patrón, a datos que son muy escasos o de rara ocurrencia? Por ejemplo: cirugías incorrectas, caídas de pacientes, días desde el último accidente, errores en estados de cuenta, días entre ausencias de cierto empleado o cierto estudiante. La frecuencia de estos eventos generalmente es muy baja y puede pasar mucho tiempo entre eventos. El Dr. James Benneyan, de Northeastern University, propuso una ingeniosa herramienta para este tipo de situaciones. Es un gráfico muy sencillo conocido como Gráfico G, así llamado porque está basado la Distribución Geométrica. Esta distribución tiene las siguientes características:
- El proceso consta de un número no definido de pruebas o experimentos separados o separables. El proceso concluirá cuando se obtenga por primera vez el resultado deseado (éxito).
- Cada prueba puede dar dos resultados mutuamente excluyentes: A y no A.
- La probabilidad de obtener un resultado A en cada prueba es p y la de obtener un resultado no A es q siendo (p + q = 1).
La genialidad del Gráfico G está en graficar el tiempo entre eventos en lugar de los eventos como tales. Vamos directo a un ejemplo reciente. Desde el año 2014 el Volcán Turrialba en Costa Rica aumentó notablemente su actividad. Veamos primero las erupciones registradas desde el año 2010 hasta la primera erupción del 2014.
| 5 de enero 2010 |
| 21 de mayo 2013 |
| 30 de octubre 2014 |
A partir del 30 de octubre del año 2014 el volcán cambia su patrón de actividad con erupciones más frecuentes. Esta vez vamos a agregar una columna que nos indique los días entre erupciones y vamos a ver el comportamiento hasta el mes de julio del 2016.
| Fecha | Días entre erupciones |
| 1/5/2010 | 0 |
| 5/21/2013 | 1232 |
| 10/30/2014 | 527 |
| 11/1/2014 | 2 |
| 12/8/2014 | 37 |
| 3/2/2015 | 84 |
| 4/5/2015 | 34 |
| 4/7/2015 | 2 |
| 4/23/2015 | 16 |
| 4/24/2015 | 1 |
| 5/4/2015 | 10 |
| 10/31/2015 | 180 |
| 5/1/2016 | 183 |
| 5/12/2016 | 11 |
| 5/18/2016 | 6 |
| 5/19/2016 | 1 |
| 5/20/2016 | 1 |
| 5/21/2016 | 1 |
| 5/24/2016 | 3 |
| 5/25/2016 | 1 |
| 5/27/2016 | 2 |
| 6/2/2016 | 6 |
| 6/3/2016 | 1 |
| 6/4/2016 | 1 |
| 6/10/2016 | 6 |
| 6/16/2016 | 6 |
| 6/19/2016 | 3 |
| 6/24/2016 | 5 |
| 7/7/2016 | 13 |
| 7/22/2016 | 15 |
| 7/25/2016 | 3 |
El Gráfico G (días entre erupciones) nos ayudará a entender mejor los datos.
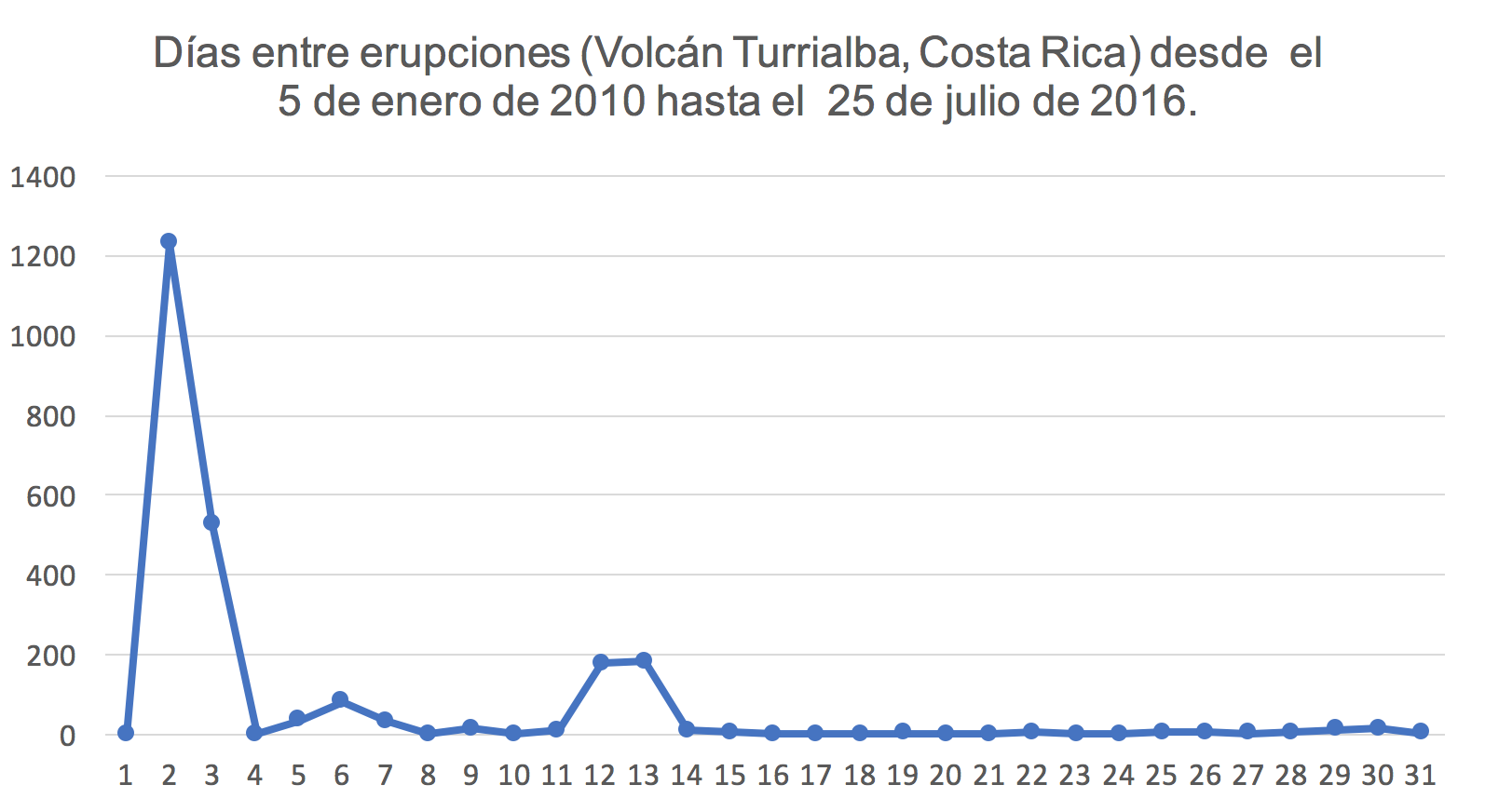Claramente se comprueba el aumento de actividad en el volcán. Los 1,232 días entre la primera y segunda erupción tienen un efecto sobre la escala, sin embargo, es claro el patrón de aumento de actividad.
¿Qué ha pasado desde julio del 2016? Lejos de menguar, el volcán se ha mantenido activo, y sigue activo hasta muy recientemente. Veamos cómo se ve el comportamiento de las erupciones hasta julio del 2017.
| Fecha | Días entre erupciones |
| 9/19/16 | 56 |
| 9/20/16 | 1 |
| 9/22/16 | 2 |
| 9/26/16 | 4 |
| 10/3/16 | 7 |
| 10/4/16 | 1 |
| 10/5/16 | 1 |
| 10/6/16 | 1 |
| 10/7/16 | 1 |
| 10/8/16 | 1 |
| 10/9/16 | 1 |
| 10/10/16 | 1 |
| 10/11/16 | 1 |
| 10/12/16 | 1 |
| 10/13/16 | 1 |
| 10/14/16 | 1 |
| 10/15/16 | 1 |
| 10/16/16 | 1 |
| 10/17/16 | 1 |
| 10/23/16 | 6 |
| 11/9/16 | 17 |
| 1/27/17 | 79 |
| 2/9/17 | 13 |
| 2/13/17 | 4 |
| 3/27/17 | 42 |
| 4/2/17 | 6 |
| 4/17/17 | 15 |
| 5/8/17 | 21 |
| 5/27/17 | 19 |
| 6/16/17 | 20 |
| 7/10/17 | 24 |
El nuevo Gráfico G nos presenta interesantes interrogantes. Veamos el gráfico.
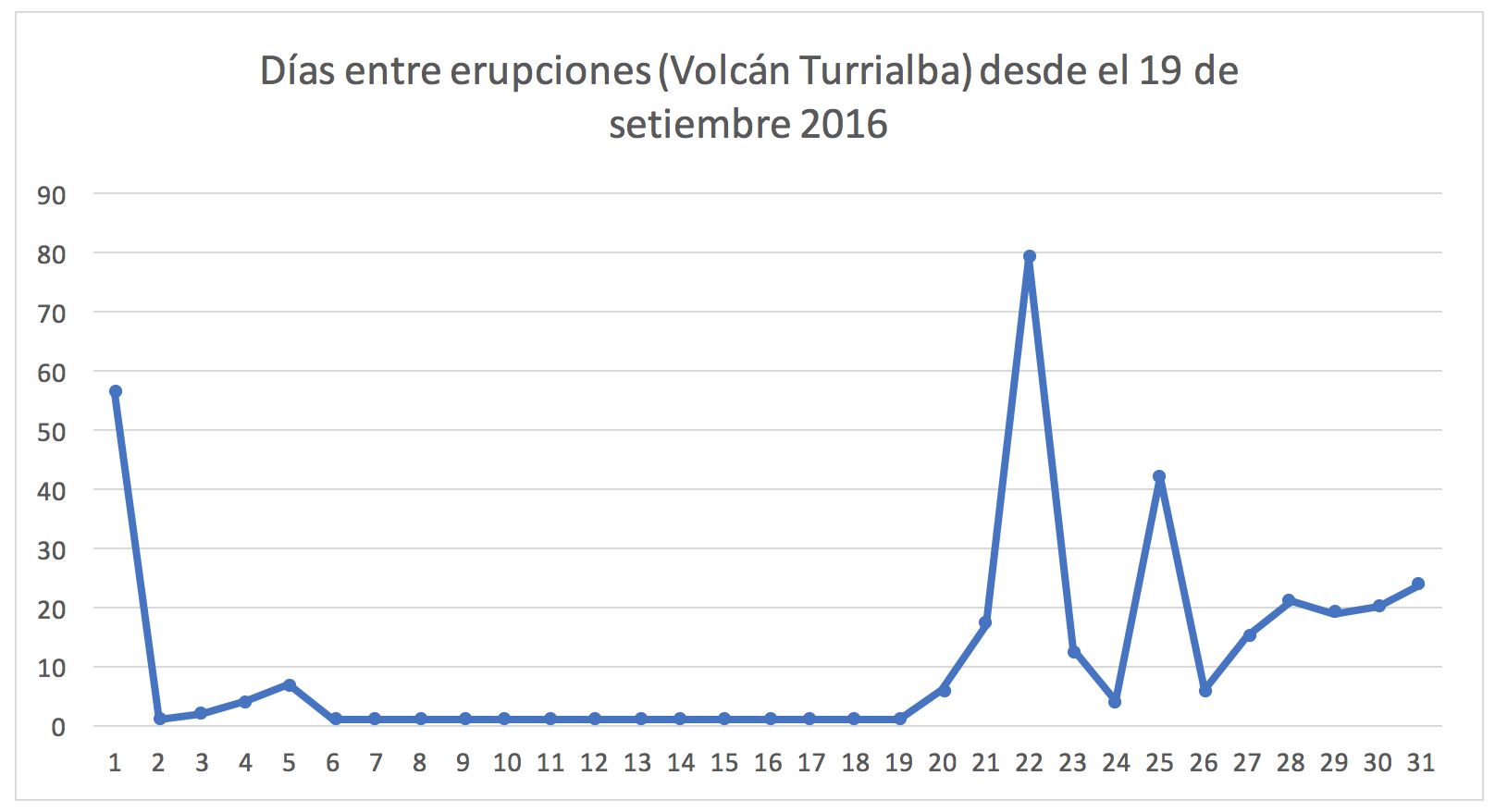
Después de un período muy intenso del 4 al 17de octubre se nota un posible cambio en el patrón, ¿será este patrón estadísticamente válido, o es muy pronto para decir si el volcán está bajando su actividad?
NOTA IMPORTANTE: para efectos de Excel, en el eje X del gráfico no se ponen las fechas sino nada más el consecutivo de eventos, en el eje Y se agregan los días entre eventos. La función para restar días entre dos fechas es =days(fecha1,fecha2). Además, el Gráfico G ha sido agregado recientemente a los softwares estadísticos comerciales de mayor uso. También se puede encontrar en los paquetes qcc y qicharts de R.
Benneyan propone límites de control basados en la teoría de Walter Shewhart (el abuelo del control de la calidad), y ese será nuestro tema de la próxima semana. Por ahora, disfruten de esta simple herramienta que nos permite investigar patrones de eventos que ocurren raramente.
