En análisis estadístico es común escuchar que una muestra de n=30 especímenes o unidades es suficiente para obtener conclusiones significativas sobre una población en estudio. En realidad, es una regla arbitraria con algunas virtudes pero que de ninguna manera sustituye al cálculo correcto de la muestra.
En esencia podemos decir que n=30 puede ser un punto de partida para calcular los primeros estadísticos, y así poder determinar el verdadero tamaño de “n” para cumplir con los objetivos de nuestra investigación.
Origen del mito n=30
1. La distribución t Student y su relación con la distribución Normal Estándar
Siempre hay algo de verdad en los mitos y leyendas. Empecemos con la distribución t de Student, o como yo la llamo “la distribución normal estándar de los pobres”, que se usa para representar datos normales cuando se tiene solamente un número limitado de muestras. Veamos qué pasa cuando el tamaño de muestra se aproxima a 30.
La curva azul representa a la distribución t Student, la curva café representa a la distribución normal estándar. Note como ambas curvas se igualan cuando n = 30.
Tamaño de muestra
Comparación entre t Student y Normal
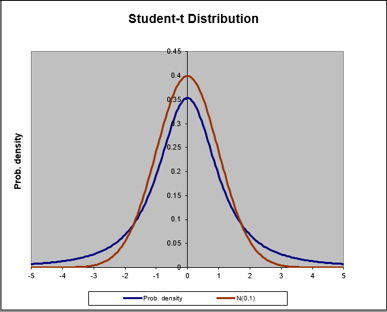
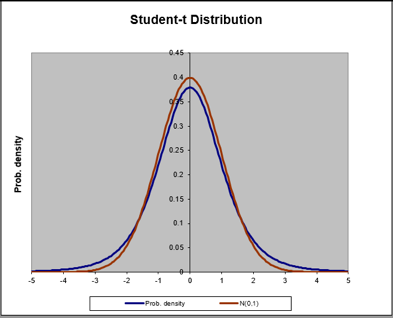
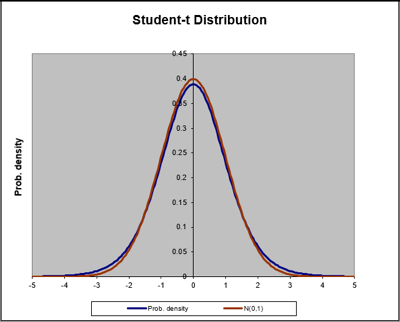
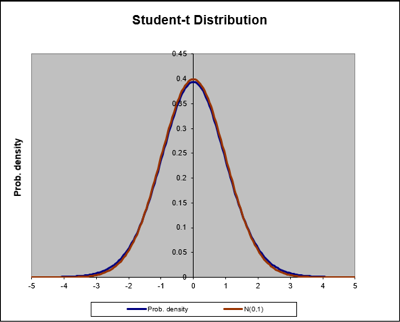
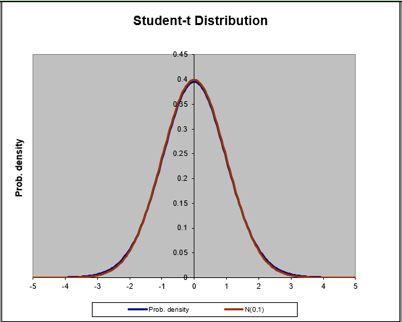
Tabla 1. Comparación entre las curvas de las distribuciones t de Student y Normal Estándar cuando n crece. NOTA: he usado este archivo de Excel por mucho años y desgraciadamente perdí la referencia en internet.
2. Ley de los grandes números y el promedio de muestras normales.
Charlie Kufs hace un excelente estudio de tamaños de muestra en su blog Stats with Cats. Según la Ley de los Grandes Números entre más grande el tamaño de muestra, más se acerca la media al promedio de la población. Ojo, no tiene nada que ver con el Teorema del Límite Central del que ya hablamos anteriormente. Me surgió la curiosidad de repetir su estudio que se resume en la siguiente figura. Primero se generaron 10,000 números aleatorios. Para efectos de mi estudio generé números distribuidos normalmente entre 1 y 100 (para eso se trabaja con una media teórica de 50 con desviación 16.67). Luego se sacaron 100 muestras de 2 unidades y se calcularon los promedios de cada muestra, 100 muestras de 5 unidades y se sacaron los promedios de cada muestra, continuando con 100 muestras de 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90 y 100 y los respectivos promedios de cada muestra. Puede verse como los mínimos y máximos son muy precisos para muestras mayores a 10 unidades, y ya en 30 unidades se puede considerar estable.
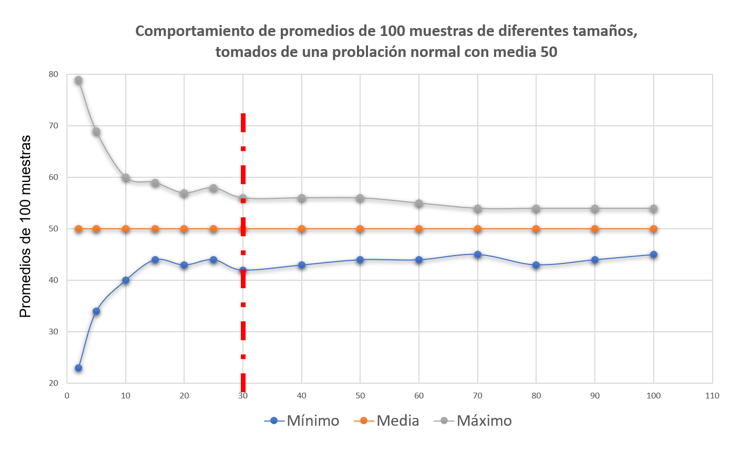
Figura 1. Comportamiento de promedios de 100 muestras para diferentes tamaños de muestra, tomados de una población normal con media 50
Nótese hasta aquí que no hemos justificado la muestra de n = 30 sino de donde proviene la leyenda. En su defensa podemos decir que, para poblaciones normales, con pocas fuentes de variación y mucho control, nos podemos animar a usar 30 para hacer estudios preliminares, pero la confirmación y validación del tamaño de muestra final depende de muchos otros factores.
Elementos para el cálculo de un tamaño de muestra estadísticamente válido
Hasta aquí tenemos que ser claros que n = 30 “no se vale” a menos que podamos justificarlo estadísticamente. La fórmula más básica de tamaño de muestra para variable continua contiene muchos elementos a considerar. Esta es la poco amigable fórmula (y es la más sencilla de todas):
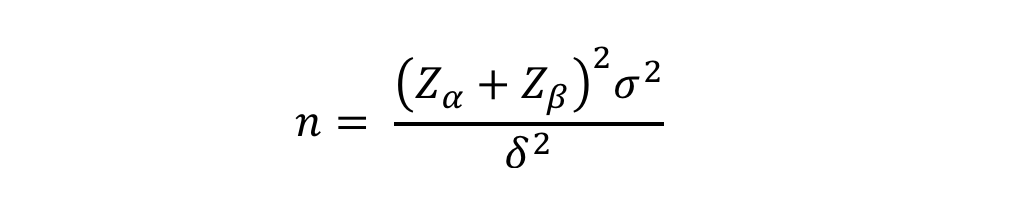
Esos elementos aseguran, hasta donde sea posible, que no estemos considerando un número tan pequeño que no detecte lo que andamos buscando, ni tan grande que nos haga gastar recursos innecesarios en pruebas, instrumentos y personal.
¿Qué tal si probamos ésta y otras fórmulas en otra ocasión, y de paso vemos qué tal se comporta nuestro querido n = 30 cuando lo pasamos por la artillería estadística pesada?
Y ya sabe, si en su empresa le dijeron que 30 es el tamaño de muestra “porque sí”, “porque el estadístico corporativo es muy inteligente”, y peor “porque el Teorema del Límite Central lo valida (¡jamás!)” tenga cuidado, puede ser que el número como tal sea suficiente, pero ninguna de esas explicaciones lo es.
E!


