Primera Parte (Las fechas de entrega)
En todo proceso, ya sea de transformación o de servicios, uno de los problemas más grandes, para tienen quienes tienen que dar una fecha estimada, en la cual se dará el servicio o se entregará el producto, es precisamente cómo asignar la esa fecha.
Independientemente de si se usa un sistema de procesar para inventario (make to stock), o para cumplir con una orden de un cliente (make to order), o si se usa el sistema de enviar las órdenes al proceso conforme se reciben (push), o si se envían cuando el proceso las requiere (pull), siempre podemos estimar una fecha de entrega a nuestros clientes que podamos cumplir.
Yo desconozco el sistema que utilizan en la CCSS para dar las citas a los pacientes que requieren una operación de cualquier tipo. Sin embargo, en algunas oportunidades
, la fecha que asignan es tan ridícula que pareciera que tienen en cola (inventario en proceso, work in process (WIP) o como quiera que le llamen) a toda la población que les toca atender en el hospital correspondiente.
Yo desconozco si ellos manejan a los pacientes, por lo que en manufactura llaman familias de producto, o si a todos los ponen en el mismo saco. Si los pacientes no utilizan (o no requieren) los mismos recursos del proceso deberían clasificarse en diferentes familias y luego estimar la fecha según la familia. Pero asumiendo que sí lo hacen como se debe, no debería ser difícil dar una fecha bien estimada.
Asumamos que una muestra representativa de un proceso muestra los siguientes datos para la fecha y el número de unidades que salen del sistema (podríamos decir que son pacientes que se van para la casa, órdenes de producción que se cierran, etc.) y obviemos lo de aleatoria y asumamos que sí es representativa.
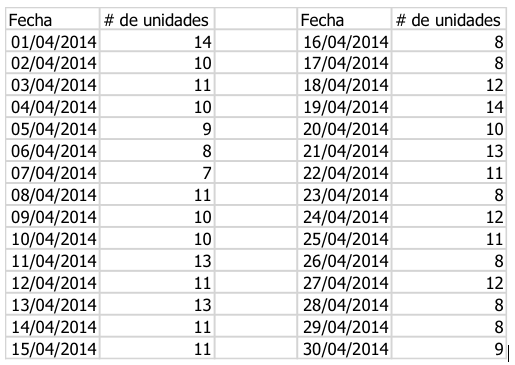Tabla 1 Unidades que salen del sistema o proceso
El resumen de estadísticos se muestra en la “Tabla 2 Resumen de estadísticos” y se muestran además el histograma de los valores y el gráfico de probabilidad normal
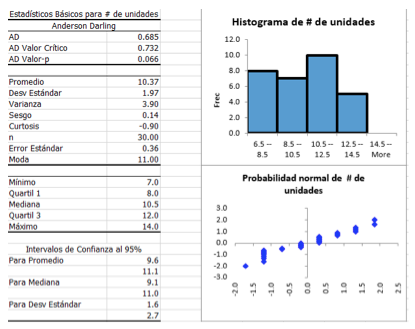Tabla 2 Resumen de estadísticos
De los datos anteriores se puede concluir que en promedio salen del sistema todos los días unas 10.4 unidades.
Con estos datos, y usando una ley llamada Ley de Little, podemos calcular la fecha en que saldrá del sistema una unidad que llega hoy. Lo único que necesitamos es saber cuántas unidades tenemos en proceso (en inventario o en WIP). Asumamos que tenemos 1200 unidades en espera y 48 en proceso para un total de 1248 unidades. El cálculo diría que una unidad que ingresa al sistema tiene que esperar para salir del mismo 1248/10.4=120 días o unos 4 meses. Si no queremos dar un estimador puntual sino que lo que se quiere es un intervalo de confianza, se podría utilizar los valores del intervalo de confianza calculados para la media, que en este caso son 9.6 en el caso pesimista y 11.1 en el caso optimista. Recalculando la fecha con éstos valores se obtiene 1248/9.6=130 días o 1248/11.1=112 días. El intervalo no se ve simétrico pero es un asunto más de redondeo que de estadística. El intervalo que se calculó se hizo a un 95% de nivel de confianza. Este valor se puede variar si se requiere otro nivel distinto.
Asumiendo que el proceso consta de tres operaciones que podemos llamar Preparación con una duración de un día, Transformación con una duración de medio día y Acabado con una duración de día y medio, el tiempo de ciclo total de una unidad en el sistema (sin tomar en cuenta la cola) es de tres días. Esto hace que el inicio del proceso se programe para tres días antes de la fecha estimada de finalización.
¿Ahora si esto se ve tan fácil dónde está el problema?
El problema no está en las fechas sino en la planeación de la capacidad de procesamiento. En nuestro caso no hemos calculado cuál es el proceso que gobierna el volumen de procesamiento (cuello de botella). Podría ser que el proceso de Preparación y Acabado tengan una capacidad mayor que 10.4 unidades por día y que fuera el proceso de Transformación el que tuviera la cifra más pequeña de 10.4. Si esto fuera así, y además fuera lo conveniente, la planificación de la capacidad debería hacerse alrededor de ese proceso y comparándolo con el tiempo Takt.
Asumiendo que la empresa calculó bien el tiempo Takt (el ritmo de la demanda) y que efectivamente es de 10.4 unidades por día, se puede decir que el proceso está balanceado y el problema de la longitud de la cola, es un problema que se arrastra debido a una planificación mal hecha en el pasado. Este parece ser el problema prevalente en todas las empresas que no se hacen una planificación adecuada de los recursos de cada proceso. En algunos casos se debe a limitaciones financieras aunque no en todos. Si una empresa desea “ponerse al día con la demanda”, es decir disminuir la longitud de la cola debe, aunque sea temporalmente, aumentar la capacidad de procesamiento hasta disminuirla a cifras razonables.
Si en este momento la empresa estuviera interesada en disminuir la cola a digamos a unos 20 días en un lapso de un año debería planificar procesar unos 12.7 unidades diarias, lo que representa un 22% más de lo que procesa hoy. Pero implicaría una reducción del tiempo de ciclo de 120 a 20 días o una reducción a un 17% del tiempo de ciclo actual.
En una ocasión posterior hablaremos sobre otros aspectos de la Ley de Little.
